题目内容
3.若直线y=kx(k>0)与双曲线y=$\frac{3}{x}$的交点为(x1,y1)、(x2,y2),则2x1y2-5x2y1的值为9.分析 (x1,y1)、(x2,y2)可代入直线y=kx以及y=$\frac{3}{x}$,然后联立各式即可求出原式的答案.
解答 解:将(x1,y1)、(x2,y2)可代入直线y=kx
∴y1=kx1,y2=kx2
∴上述两式相除可得:x1y2=x2y1,
将(x1,y1)、(x2,y2)可代入直线y=$\frac{3}{x}$,
∴x1y1=3,x2y2=3,
上述两式相乘,x1x2y1y2=9,
∴(x1y2)2=9,
∴x1y2=±3
∵k>0,
∴直线y=kx与双曲线y=$\frac{3}{x}$在第一、三象限,
若x1>0时,则y2<0,
∴x1y2=-3,
∴原式=2x1y2-5x1y2=-3x1y2=9,
故答案为:9
点评 本题考查反比例函数与一次函数的交点,解题的关键是将交点坐标代入解析式中,联立各式求解,本题综合程度较高,属于中等题型.

练习册系列答案
相关题目
13.下列算式能用平方差公式计算的是( )
| A. | (3a+b)(3b-a) | B. | ($\frac{1}{3}$x-1)(1+$\frac{1}{3}$x) | C. | (2x-y)(-2x+y) | D. | (-s-t)(-s-t) |
 如图,已知平面坐标系中,A(-1,5),B(2,0),C(-3,-1).
如图,已知平面坐标系中,A(-1,5),B(2,0),C(-3,-1).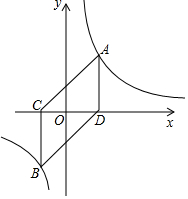 如图,O为坐标原点,点A在第一象限,且在函数y=$\frac{2}{x}$的图象上.延长AO,交双曲线于另一点B,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接AC、BD.(注:不能用双曲线关于原点对称解答下列问题)
如图,O为坐标原点,点A在第一象限,且在函数y=$\frac{2}{x}$的图象上.延长AO,交双曲线于另一点B,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接AC、BD.(注:不能用双曲线关于原点对称解答下列问题)