题目内容
18．一元二次方程x2-2x+m=0总有实数根，则m应满足的条件是（ ）| A． | m=1 | B． | m≥1 | C． | m＜1 | D． | m≤1 |
分析 根据根的判别式，令△≥0，建立关于m的不等式，解答即可．
解答 解：∵方程x2-2x+m=0总有实数根，
∴△≥0，
即4-4m≥0，
∴-4m≥-4，
∴m≤1．
故选：D．
点评 本题考查了根的判别式，一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
8．若m是任意实数，则点M（m2+2，-2）在第（ ）象限．
| A． | 一 | B． | 二 | C． | 三 | D． | 四 |
9．
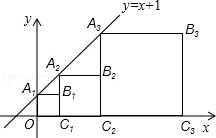正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点B2016的纵坐标是（ ）
正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点B2016的纵坐标是（ ）| A． | 22013 | B． | 22014 | C． | 22015 | D． | 22016 |
6．
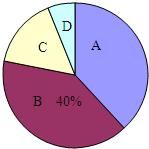某市共有45000余名学生参加中考体育测试，为了了解九年级男生立定跳远的成绩成绩，从某校随机抽取了50名男生的测试成绩，根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成扇形图和统计表：
请你根据以上图表提供的信息，解答下列问题：
（1）m=20，n=8，x=0.4，y=0.16；
（2）在扇形图中，C等级所对应的圆心角是57.6度；
（3）如果该校九年级共有500名男生，则其中成绩等级达到优秀和良好的共有多少人？
某市共有45000余名学生参加中考体育测试，为了了解九年级男生立定跳远的成绩成绩，从某校随机抽取了50名男生的测试成绩，根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成扇形图和统计表：| 等级 | 成绩（分） | 频数（人数） | 频率 |
| A | 90～100 | 19 | 0.38 |
| B | 75～89 | m | x |
| C | 60～74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
（1）m=20，n=8，x=0.4，y=0.16；
（2）在扇形图中，C等级所对应的圆心角是57.6度；
（3）如果该校九年级共有500名男生，则其中成绩等级达到优秀和良好的共有多少人？
13．下列从左到右的变形，是因式分解的是（ ）
| A． | （3-x）（3+x）=9-x2 | B． | （y+1）（y-3）=（3-y）（y+1） | ||
| C． | 4yz-2y2z+z=2y（2z-zy）+z | D． | -8x2+8x-2=-2（2x-1）2 |
3．
如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行，从内到外，它们的边长依次为2，4，6，8，…，顶点一次用A1，A2，A3，A4，…表示，则顶点A2016的坐标是（ ）
如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行，从内到外，它们的边长依次为2，4，6，8，…，顶点一次用A1，A2，A3，A4，…表示，则顶点A2016的坐标是（ ）| A． | （504，504） | B． | （-504，504） | C． | （-504，-504） | D． | （504，-504） |
10．已知函数y=$\frac{1}{x-3}$，自变量x的取值范围是（ ）
| A． | x≠3且x≠0 | B． | x＞3 | C． | x＜3 | D． | x≠3 |
7．已知一次函数y=kx+b的图象经过点（-2，-6），（0，4），则当y=0时，x的值为（ ）
| A． | $-\frac{2}{5}$ | B． | $-\frac{4}{5}$ | C． | $\frac{4}{5}$ | D． | $\frac{2}{5}$ |
8．下列图形是中心对称而不是轴对称的是（ ）
| A． |  | B． |  | C． |  | D． |  |