题目内容
1．
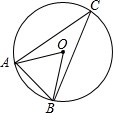已知：如图，AO、BO是⊙O的两条半径，点C在⊙O上，∠ACB=30°，则∠ABO的度数为（ ）| A． | 30° | B． | 45° | C． | 50° | D． | 60° |
分析 根据圆周角定理求出∠AOB，根据等腰三角形性质得出∠OBA=∠OAB，根据三角形内角和定理求出即可．
解答 解：∵∠ACB=30°，
∴∠AOB=2∠ACB=60°，
∵OA=OB，
∴∠ABO=∠BAO=$\frac{1}{2}$×（180°-∠AOB）=60°，
故选D．
点评 本题考查了圆周角定理，等腰三角形性质，三角形的内角和定理的应用，解此题的关键是求出∠AOB度数和得出∠OAB=∠OBA．
练习册系列答案
相关题目
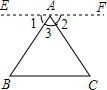已知△ABC，求证∠A+∠B+∠C=180°．请在括号里填上适当的理由．
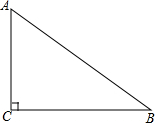如图，在Rt△ABC中，∠C=90°，sinB=$\frac{3}{5}$，BC=5cm，以点C为圆心，以3cm的长为半径作圆，则⊙C与AB的位置关系是（ ）
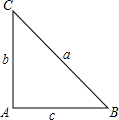已知△ABC中，∠A=2∠B，∠A=90°，求证：a2-b2=bc．
已知：如图，在平行四边形ABCD中，E、F分别是边AB和DC上的点，且BE=DF．求证：AF=CE．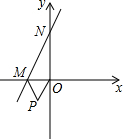
如图，已知直线y=2x+6与x轴、y轴分别交于M，N两点，以OM为边在x轴下方作等边三角形OMP，现将△OMP沿y轴向上平移，当点P恰好落在直线MN上时，点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3．
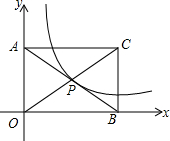如图，矩形AOBC的面积为8，反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P，则反比例函数的解析式为y=$\frac{2}{x}$．
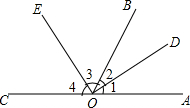∠AOB与∠BOC互为补角，OD平分∠AOB，∠3+∠2=90°，如图所示．求证∠BOE=$\frac{1}{2}$∠BOC．请完成下列证明．