题目内容
12.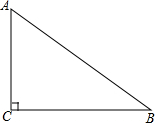 如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相切或相交 |
分析 利用锐角三角函数关系以及勾股定理得出AC,BC的长,再利用三角形面积求出DC的长,进而利用直线与圆的位置关系得出答案.
解答 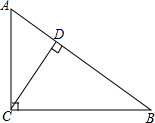 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
∵∠C=90°,sinB=$\frac{3}{5}$,
∴设AC=3xcm,AB=5xcm,
故在Rt△ABC中,AC2+BC2=AB2,
即(3x)2+52=(5x)2,
解得:x=$\frac{5}{4}$,
则AC=$\frac{15}{4}$cm,AB=$\frac{25}{4}$cm,
故S△ACB=$\frac{1}{2}$AC×BC=$\frac{1}{2}$DC×AB,
即$\frac{1}{2}$×$\frac{15}{4}$×5=$\frac{1}{2}$×DC×$\frac{25}{4}$,
解得:DC=3,
故以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是相切.
故选:C.
点评 此题主要考查了勾股定理以及锐角三角函数关系、三角形面积求法等知识,得出Rt△ABC斜边上的高是解题关键.

练习册系列答案
相关题目
3.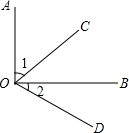 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )| A. | 直角都相等 | B. | 等角的余角相等 | C. | 同角的余角相等 | D. | 同角的补角相等 |
20.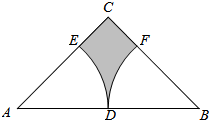 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )| A. | 2-π | B. | 3-π | C. | 3.5-π | D. | 4-π |
7.下列说法正确的是( )
| A. | 为了解2016年春节联欢晚会收视情况,应采用全面调查方式 | |
| B. | 为了解全国中学生的视力状况,应采用普查方式 | |
| C. | 乘坐高铁时,检查旅客行李是否携带有违禁物品应采用抽样调查方式 | |
| D. | 为了解2016年春节中国人最喜欢的过年方式应采用抽样调查方式 |
4.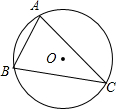 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}$ |
1.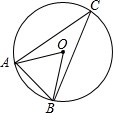 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
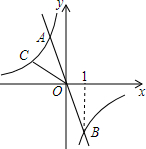 已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).
已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).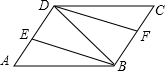 如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F. 已知△A′B′C′是由△ABC经过顺时针旋转而得.
已知△A′B′C′是由△ABC经过顺时针旋转而得.