题目内容
6. 已知:如图,在平行四边形ABCD中,E、F分别是边AB和DC上的点,且BE=DF.求证:AF=CE.
已知:如图,在平行四边形ABCD中,E、F分别是边AB和DC上的点,且BE=DF.求证:AF=CE.
分析 因为ABCD是平行四边形,所以AB=CD,AB∥CD,已知BE=DF,从而可得到AE=CF,再根据有一组边平行且相等的四边形是平行四边形推出CFAF是平行四边形,从而不难得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵BE=DF,
∴AE=CF,
∵AB∥CD,
∴四边形CEAF是平行四边形,
∴AF=CE.
点评 此题主要考查学生对平行四边形的性质及判定的理解及运用能力;灵活运用平行四边形的判定方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.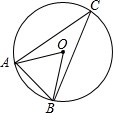 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
18.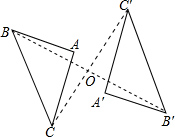 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )| A. | ∠ABC=∠A′B′C′ | B. | ∠BOC=∠B′A′C′ | C. | AB=A′B′ | D. | OA=OA′ |
16.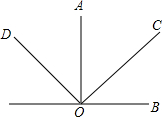 如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
 如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )| A. | 180°-2α | B. | 180°-α | C. | 90°+$\frac{1}{2}$α | D. | 2α-90° |

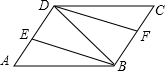 如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F. 如图,AD是⊙O的直径,弦BC⊥AD,连接AB、AC、OC,若∠COD=60°,则∠BAD=30°.
如图,AD是⊙O的直径,弦BC⊥AD,连接AB、AC、OC,若∠COD=60°,则∠BAD=30°. 如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
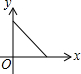
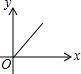
如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )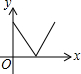
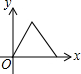
 画出该几何体的三视图:
画出该几何体的三视图: