题目内容
10.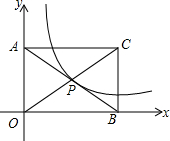 如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$.
如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$.
分析 作PE⊥x轴,PF⊥y轴,根据矩形的性质得矩形OEPF的面积=$\frac{1}{4}$矩形AOBC的面积=$\frac{1}{4}$×8=2,然后根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义即可得到k=2.
解答 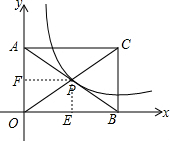 解:如图,作PE⊥x轴,PF⊥y轴.
解:如图,作PE⊥x轴,PF⊥y轴.
∵点P为矩形AOBC对角线的交点,
∴矩形OEPF的面积=$\frac{1}{4}$矩形AOBC的面积=$\frac{1}{4}$×8=2,
∴|k|=2,
而k>0,
∴k=2,
∴过P点的反比例函数的解析式为y=$\frac{2}{x}$.
故答案为:y=$\frac{2}{x}$.
点评 本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
相关题目
20.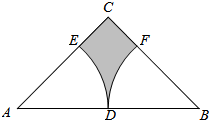 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )| A. | 2-π | B. | 3-π | C. | 3.5-π | D. | 4-π |
1.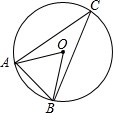 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
18.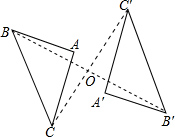 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )| A. | ∠ABC=∠A′B′C′ | B. | ∠BOC=∠B′A′C′ | C. | AB=A′B′ | D. | OA=OA′ |
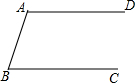 如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法).
如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法). 画出该几何体的三视图:
画出该几何体的三视图: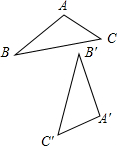 已知△A′B′C′是由△ABC经过顺时针旋转而得.
已知△A′B′C′是由△ABC经过顺时针旋转而得.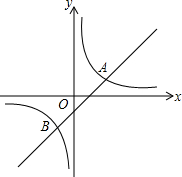 如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)
如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)