题目内容
9.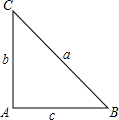 已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc.
已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc.
分析 设∠B=x,则∠A=2x,根据∠A=90°,得关于x的方程,再得出结论即可.
解答 解:∵∠A=2∠B,
∴设∠B=x,则∠A=2x,
∵∠A=90°,
∴x=45°,
∴b=c,
∵∠A=90°,
∴b2+c2=a2,
∴a2-b2=b2+c2-b2=c2,
∴bc=c2,
∴a2-b2=bc.
点评 本题考查了等腰直角三角形,以及勾股定理,掌握等腰三角形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.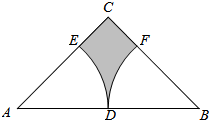 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )| A. | 2-π | B. | 3-π | C. | 3.5-π | D. | 4-π |
4.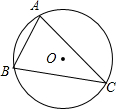 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}$ |
1.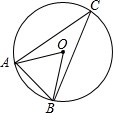 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
18.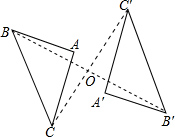 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )| A. | ∠ABC=∠A′B′C′ | B. | ∠BOC=∠B′A′C′ | C. | AB=A′B′ | D. | OA=OA′ |
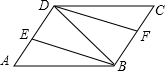 如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F. 如图,AD是⊙O的直径,弦BC⊥AD,连接AB、AC、OC,若∠COD=60°,则∠BAD=30°.
如图,AD是⊙O的直径,弦BC⊥AD,连接AB、AC、OC,若∠COD=60°,则∠BAD=30°.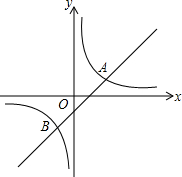 如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)
如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)