题目内容
11.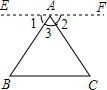 已知△ABC,求证∠A+∠B+∠C=180°.请在括号里填上适当的理由.
已知△ABC,求证∠A+∠B+∠C=180°.请在括号里填上适当的理由.证明:过点A作直线EF∥BC
∴∠1=∠B,∠2=∠C两直线平行,内错角相等
∵EF是一条直线
∴∠EAF=180°平角的定义
又∵∠EAF=∠1+∠2+∠3
∴∠1+∠2+∠3=180°平角的定义
∴∠3+∠B+∠C=180°等量代换.
分析 过点A作直线EF∥BC,则∠B=∠1,∠2=∠C,再根据平行线的性质解答即可.
解答 证明:过点A作直线EF∥BC,
∴∠1=∠B,∠2=∠C(两直线平行,内错角相等),
∵EF是一条直线
∴∠EAF=180°(平角的定义),
又∵∠EAF=∠1+∠2+∠3
∴∠1+∠2+∠3=180° (平角的定义),
∴∠3+∠B+∠C=180°(等量代换),
故答案为:两直线平行,内错角相等;平角的定义;平角的定义;等量代换
点评 此题考查平行线的性质,解答此题的关键是过点A作直线EF∥BC,利用平行线的性质解答.

练习册系列答案
相关题目
3.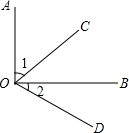 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )| A. | 直角都相等 | B. | 等角的余角相等 | C. | 同角的余角相等 | D. | 同角的补角相等 |
20.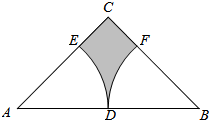 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )| A. | 2-π | B. | 3-π | C. | 3.5-π | D. | 4-π |
1.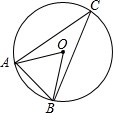 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
 已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )
已知:如图,AO、BO是⊙O的两条半径,点C在⊙O上,∠ACB=30°,则∠ABO的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
 已知:如图,AC=EC,E、A、D在同一条直线上,∠1=∠2=∠3.试说明:△ABC≌△EDC.
已知:如图,AC=EC,E、A、D在同一条直线上,∠1=∠2=∠3.试说明:△ABC≌△EDC.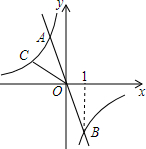 已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).
已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).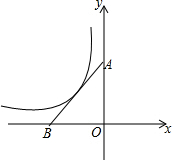 如图,在平面直角坐标系中,点A,B分别在y轴的正半轴和x轴的负半轴上,Rt△AOB的面积是4,若反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点,则k的值是-2.
如图,在平面直角坐标系中,点A,B分别在y轴的正半轴和x轴的负半轴上,Rt△AOB的面积是4,若反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点,则k的值是-2.