题目内容
9.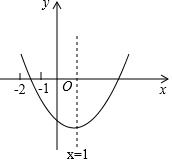 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则$\frac{b}{a}$的值为-2;$\frac{c}{a}$的取值范围为-8<$\frac{c}{a}$<-3.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则$\frac{b}{a}$的值为-2;$\frac{c}{a}$的取值范围为-8<$\frac{c}{a}$<-3.
分析 根据抛物线的对称轴为x=1可得$\frac{b}{a}$=-2,由当x=-2时y>0,即4a-2b+c>0 ①,当x=-1时y<0,即a-b+c<0 ②,将b=-2a代入可得$\frac{c}{a}$的取值范围.
解答 解:∵抛物线的对称轴为直线x=1,
∴x=-$\frac{b}{2a}$=1,即$\frac{b}{a}$=-2;
∵当x=-2时,y>0,即4a-2b+c>0 ①,
当x=-1时,y<0,即a-b+c<0 ②,
将b=-2a代入①、②得:c>-8a,c<-3a,
又∵a>0,
∴-8<$\frac{c}{a}$<-3,
故答案为:-2,-8<$\frac{c}{a}$<-3.
点评 本题考查了抛物线图象与系数的关系,其中a由抛物线的开口方向决定,a与b同号对称轴在y轴左边;a与b异号对称轴在y轴右边,c的符合由抛物线与y轴的交点在正半轴或负半轴有关.

练习册系列答案
相关题目
19.若$\frac{{3\sqrt{x+1}}}{x-2}$有意义,则x应满足的条件是( )
| A. | x≠-1 | B. | x≥2 | C. | x≠2 | D. | x≥-1且x≠2 |
20.在平面内过O点作三条射线OA、OB、OC,已知∠AOB=50°,∠BOC=20°,则∠AOC的度数为( )
| A. | 70° | B. | 30° | C. | 70°或30° | D. | 无法确定 |
17.2008年5月18日晚,中央电视台举办了“爱的奉献”大型募捐活动.据了解,本次活动社会各界共向四川灾区捐款大约1510000000元人民币,这个数字用科学记数法可表示为1.51×109元人民币.
14.下列说法正确的是( )
| A. | 将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则此时抛物线的解析式是y=(x+4)2-2 | |
| B. | 方程x2+2x+3=0有两个不相等的实数根 | |
| C. | 平行四边形既是中心对称图形又是轴对称图形 | |
| D. | 平分弦的直径垂直于弦,并且平分这条弦所对的两条弧 |
18. 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )| A. | x<3 | B. | x>2 | C. | x<5 | D. | x>5 |
19.已知二次函数y=ax2+bx+c的图象分别与坐标轴交于A,B,C三点,且OA=OB=OC,则一次函数y=(a-c)x+ac-c的图象一定经过( )
| A. | 一、二、三象限 | B. | 一、三、四象限 | C. | 一、二、四象限 | D. | 二、三、四象限 |
 我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.
我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.