题目内容
19.已知二次函数y=ax2+bx+c的图象分别与坐标轴交于A,B,C三点,且OA=OB=OC,则一次函数y=(a-c)x+ac-c的图象一定经过( )| A. | 一、二、三象限 | B. | 一、三、四象限 | C. | 一、二、四象限 | D. | 二、三、四象限 |
分析 由题目的条件可画出二次函数图象的草图,根据图象可得到a,b,c的正负情况,所以一次函数y=(a-c)x+ac-c各项的系数可以确定,进而可知道其图象经过的象限.
解答 解:
∵二次函数y=ax2+bx+c的图象分别与坐标轴交于A,B,C三点,且OA=OB=OC,
∴函数图象如图所示:
当a>0时,则b=0,c<0,
所以a-c>0,ac-c<0或ac-c≥0,
即一次函数y=(a-c)x+ac-c的图象一定经过一、三、四象限或一、二、三象限或一、三象限,
当a<0时,则b=0,c>0,
所以a-c<0,ac-c<0,
即一次函数y=(a-c)x+ac-c的图象一定经过二、三、四象限;
所以一次函数y=(a-c)x+ac-c的图象一定经过过二、三、四象限,
故选D.
点评 本题考查了抛物线和x轴交点的问题,能够准确画出二次函数图象的具体位置是解题的关键.

练习册系列答案
相关题目
7.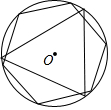 图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
 图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )| A. | $\sqrt{6}$:2 | B. | $\sqrt{3}$:2 | C. | $\sqrt{3}$:1 | D. | 2:1 |
18.等腰三角形的一个角是100°,则它的顶角的度数是( )
| A. | 100° | B. | 100°或20° | C. | 100°或50° | D. | 20° |
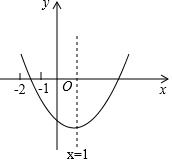 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则$\frac{b}{a}$的值为-2;$\frac{c}{a}$的取值范围为-8<$\frac{c}{a}$<-3.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则$\frac{b}{a}$的值为-2;$\frac{c}{a}$的取值范围为-8<$\frac{c}{a}$<-3.