题目内容
4. 我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.
我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.(1)求y与x之间的函数关系式;
(2)老张种植柑橘的成本是800元/吨,当客商采购量是多少时,老张在这次销售柑橘时获利最大?最大利润是多少?
分析 (1)分别根据当0<x≤10时,y=2000,当10<x≤20时,设函数关系式为y=kx+b,分别求出即可;
(2)利用当0<x≤10时,老张获得的利润为:w=(2000-1200)x,当10<x≤20时,老张获得的利润为w=(-80x+28 00-800)x分别求出即可.
解答 解:(1)当0<x≤10时,y=2000.
当10<x≤20时,设BC满足的函数关系式为y=kx+b,
∴$\left\{\begin{array}{l}{10k+b=2000}\\{20k+b=1200}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-80}\\{b=2800}\end{array}\right.$,
∴y与x之间的函数关系式为:y=-80x+2800.
(2)当0<x≤10时,老张获得的利润为:
w=(2000-800)x
=1200x≤12 000,此时老张获得的最大利润为12 000元.
当10<x≤20时,老张获得的利润为w=(-80x+2800-800)x
=-80(x2-25x)=-80(x-12.5)2+12500.
∴当x=12.5时,利润w取得最大值,最大值为12500元.
∵12500>12 000,
∴当客商的采购量为12.5吨时,老张在这次买卖中所获得的利润最大,最大利润为12500元.
点评 此题主要考查了二次函数的应用以及分段函数的应用,根据数形结合以及分类讨论得出是解题关键.

练习册系列答案
相关题目
14.下列各数中的无理数是( )
| A. | $\frac{22}{7}$ | B. | $\sqrt{9}$ | C. | 3.1415927 | D. | $2\sqrt{2}$ |
15.若x2+mxy+16y2是完全平方式,则m的值为( )
| A. | 4 | B. | ±4 | C. | 8 | D. | ±8 |
12.已知反比例函数y=-$\frac{4}{x}$,则下列有关该函数的说法正确的是( )
| A. | 该函数的图象经过点(2,2) | B. | 该函数的图象位于第一、三象限 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x>-1时,y>4 |
19. 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )
 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )| A. | ∠1=∠2 | B. | ∠1+∠2=90° | C. | ∠1+∠2=180° | D. | 不能确定 |
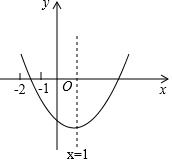 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则$\frac{b}{a}$的值为-2;$\frac{c}{a}$的取值范围为-8<$\frac{c}{a}$<-3.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则$\frac{b}{a}$的值为-2;$\frac{c}{a}$的取值范围为-8<$\frac{c}{a}$<-3.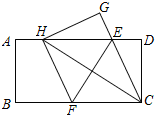 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论: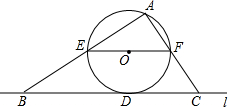 如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为$\frac{7}{5}$.
如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为$\frac{7}{5}$.