题目内容
1．函数y=$\frac{x-1}{3x+1}$中，自变量x的取值范围是x≠-$\frac{1}{3}$．分析 根据分母不等于0列式计算即可得解．
解答 解：由题意得，3x+1≠0，
解得x≠-$\frac{1}{3}$．
故答案为：x≠-$\frac{1}{3}$．
点评 本题考查了函数自变量的范围，一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
12．已知反比例函数y=-$\frac{4}{x}$，则下列有关该函数的说法正确的是（ ）
| A． | 该函数的图象经过点（2，2） | B． | 该函数的图象位于第一、三象限 | ||
| C． | 当x＞0时，y的值随x的增大而增大 | D． | 当x＞-1时，y＞4 |
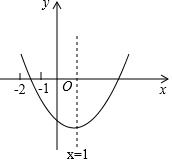二次函数y=ax2+bx+c（a≠0）的图象如图所示，则$\frac{b}{a}$的值为-2；$\frac{c}{a}$的取值范围为-8＜$\frac{c}{a}$＜-3．
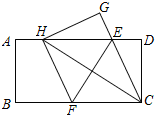如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：
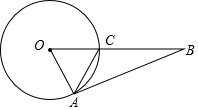如图，OA，OC都是⊙O的半径，点B在OC的延长线上，BA与⊙O相切于点A，连接AC，若AC=2，tan∠BAC=$\frac{1}{2}$，则⊙O的半径长为$\sqrt{5}$．
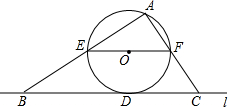如图，直线l与⊙相切于点D，过圆心O作EF∥l交⊙O于E、F两点，点A是⊙O上一点，连接AE，AF，并分别延长交直线于B、C两点；若⊙的半径R=5，BD=12，则∠ACB的正切值为$\frac{7}{5}$．