题目内容
6.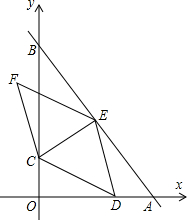 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为$\frac{56}{57}$.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为$\frac{56}{57}$.
分析 设C(0,m).由DF∥AB,CF=BF=DE=$\frac{8-m}{2}$,根据cos∠CBE=$\frac{BE}{BC}$=$\frac{OB}{AB}$=$\frac{8}{10}$,可得BE=$\frac{4}{5}$(8-m),推出AE=10-$\frac{4}{5}$(8-m),由DE∥OB,推出∠ADE=∠AOB=90°,推出sin∠DAE=$\frac{DE}{AE}$=$\frac{OB}{AB}$=$\frac{4}{5}$,可得$\frac{\frac{8-m}{2}}{10-\frac{4}{5}(8-m)}$=$\frac{4}{5}$,解方程即可解决问题.
解答 解:如图,设C(0,m).
∵四边形EFCD是菱形,
∴DF⊥CE,CP=PE,
∵CE⊥AB,
∴DF∥AB,CF=BF=DE=$\frac{8-m}{2}$,
∵cos∠CBE=$\frac{BE}{BC}$=$\frac{OB}{AB}$=$\frac{8}{10}$,
∴BE=$\frac{4}{5}$(8-m),
∴AE=10-$\frac{4}{5}$(8-m),
∵DE∥OB,
∴∠ADE=∠AOB=90°,
∴sin∠DAE=$\frac{DE}{AE}$=$\frac{OB}{AB}$=$\frac{4}{5}$,
∴$\frac{\frac{8-m}{2}}{10-\frac{4}{5}(8-m)}$=$\frac{4}{5}$,
∴m=$\frac{56}{57}$,
故答案为$\frac{56}{57}$.
点评 本题考查菱形的性质、坐标与图形的性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
18.在下列-$\sqrt{2}$,-1,0,1四个数中,最小的是( )
| A. | -$\sqrt{2}$ | B. | -1 | C. | 0 | D. | 1 |
 求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.
求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.
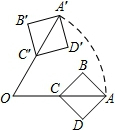 如图,线段OA=4,点C是OA的中点,以线段CA为对角线作正方形ABCD.将线段OA绕点O向逆时针方向旋转60°,得到线段OA′和正方形A′B′C′D′.在旋转过程中,正方形ABCD扫过的面积是2π+2.(结果保留π)
如图,线段OA=4,点C是OA的中点,以线段CA为对角线作正方形ABCD.将线段OA绕点O向逆时针方向旋转60°,得到线段OA′和正方形A′B′C′D′.在旋转过程中,正方形ABCD扫过的面积是2π+2.(结果保留π)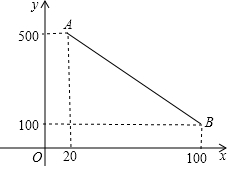 小明家买了一台充电式自动扫地机,每次完成充电后,在使用时扫地机会自动根据设定扫地时间,来确定扫地的速度(以使每次扫地结束时尽量把所储存的电量用完),如图是“设定扫地时间”与“扫地速度”之间的函数图象(线段AB),其中设定扫地时间为x分钟,扫地速度为y平方分米/分钟.
小明家买了一台充电式自动扫地机,每次完成充电后,在使用时扫地机会自动根据设定扫地时间,来确定扫地的速度(以使每次扫地结束时尽量把所储存的电量用完),如图是“设定扫地时间”与“扫地速度”之间的函数图象(线段AB),其中设定扫地时间为x分钟,扫地速度为y平方分米/分钟.