题目内容
1．
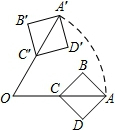如图，线段OA=4，点C是OA的中点，以线段CA为对角线作正方形ABCD．将线段OA绕点O向逆时针方向旋转60°，得到线段OA′和正方形A′B′C′D′．在旋转过程中，正方形ABCD扫过的面积是2π+2．（结果保留π）
分析 如图，用大扇形的面积减去小扇形的面积再加上正方形ABCD的面积．
解答 
解：∵OA=4，
∴OC=AC=2，
∴AB=BC=CD=AD=$\sqrt{2}$，OA=4，
S阴影=$\frac{60}{360}$π（42-22）+（$\sqrt{2}$）2=2π+2，
故答案为：2π+2．
点评 此题考查了扇形的面积公式和旋转的性质以及勾股定理，能够把不规则图形的面积转换为规则图形的面积是解答此题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
9．
如图，AB∥CD，AE交CD于点C，DE⊥AE于点E，若∠A=42°，则∠D=（ ）
如图，AB∥CD，AE交CD于点C，DE⊥AE于点E，若∠A=42°，则∠D=（ ）| A． | 42° | B． | 58° | C． | 52° | D． | 48° |
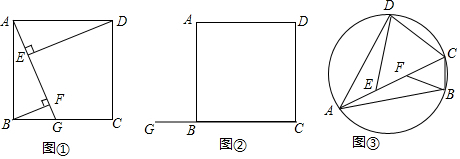
16．
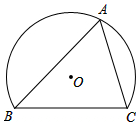如图，弓形ABC中，∠BAC=60°，BC=2$\sqrt{3}$．若点P在优弧BAC上由点B移动到点C，记△PBC的内心为I，点I随点P的移动所经过的路径长为（ ）
如图，弓形ABC中，∠BAC=60°，BC=2$\sqrt{3}$．若点P在优弧BAC上由点B移动到点C，记△PBC的内心为I，点I随点P的移动所经过的路径长为（ ）| A． | $\frac{2}{3}$π | B． | $\frac{4}{3}$π | C． | $\frac{8}{3}$π | D． | 4π |
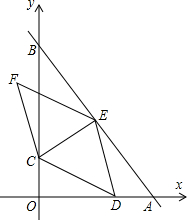如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C在OB上运动，过点C作CE⊥AB于点E；D是x轴上一点，作菱形CDEF，当顶点F恰好落在y轴正半轴上时，点C的纵坐标的值为$\frac{56}{57}$．
我国古代数学中有一道数学题：如图，有一棵枯树直立在地上，树高20尺，粗3尺，有一根藤条从树根处缠绕而上，缠绕5周到达树顶，则这条树藤有25尺．