题目内容
11.对于每个正整数n,设f(n)表示n(n+1)的末位数字,例如:f(1)=2(1×2的末尾数字),f(2)=6 (2×3的末位数字),f(3)=2(3×4的末位数字),…,则f(1)+f(2)+f(3)+…f(2016)=4032.分析 首先根据已知得出规律,f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,…,进而求出即可.
解答 解:∵f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,
…,
∴每5个数一循环,分别为2,6,2,0,0…,
∴2016÷5=403…1,
∴f(1)+f(2)+f(3)+…+f(2016)
=2+6+2+0+0+2+6+2+…+2
=403×(2+6+2)+2
=4032.
故答案为:4032.
点评 此题主要考查了数字变化规律,根据已知得出数字变化以及求出f(1)+f(2)+f(3)+…+f(2016)=403×(2+6+2)+2是解题关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.下列计算正确的是( )
| A. | 2a2•a=3a3 | B. | (2a)2÷a=4a | C. | (-3a)2=3a2 | D. | (a-b)2=a2-b2 |
3.计算$\frac{1}{2}$-$\frac{1}{2}$×3的结果是( )
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
 如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0),B(3,0).探究:抛物线y=x2-2mx+m2-4(m为常数)交x轴于点M,N两点;
如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0),B(3,0).探究:抛物线y=x2-2mx+m2-4(m为常数)交x轴于点M,N两点;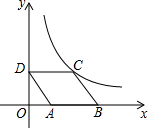 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).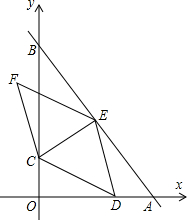 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为$\frac{56}{57}$.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为$\frac{56}{57}$.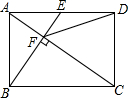 在矩形ABCD中,点E为AD的中点,连接BE、AC,AC⊥BE于点F,连接DF,则下列结论正确的有②③④.
在矩形ABCD中,点E为AD的中点,连接BE、AC,AC⊥BE于点F,连接DF,则下列结论正确的有②③④.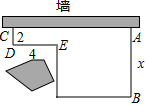 用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题:
用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题: