题目内容
2.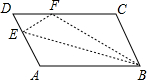 如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为6.
如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为6.
分析 根据翻折不变性以及平行四边形的性质,由BF+BC+CF=28,BF=AB=DF+FC,BC=AD=ED+EF,进行等量代换即可解决.
解答 解: ∵△BEF是由△BEA翻折,
∵△BEF是由△BEA翻折,
∴EA=EF,BF=BA,
∵四边形ABCD是平行四边形,
∴BC=AD=AE+DE=EF+ED,AB=BF=DC=DF+CF,
∵CF+BC+BF=28,DE+EF+DF=16
∴CF+DE+EF+DF+CF=28,
∴2CF+16=28,
∴CF=6,
故答案为6.
点评 本题考查翻折变换、平行四边形的性质,解题的关键是利用翻折不变性解决问题,学会整体代入的数学思想,属于中考常考题型.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
10.在平面直角坐标系中,已知点A(2,m)和点B(n,-3)关于x轴对称,则m+n的值是( )
| A. | -1 | B. | 1 | C. | 5 | D. | -5 |
17.下列图形中,既是中心对称图形又是轴对称图形的有( )个.
①线段;②等边三角形;③矩形;④菱形;⑤五角星;⑥圆.
①线段;②等边三角形;③矩形;④菱形;⑤五角星;⑥圆.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
11.若a>b,则$\sqrt{{a}^{2}}-b$的值为一定( )
| A. | 大于0 | B. | 小于0 | C. | 大于或等于0 | D. | 小于或等于0 |

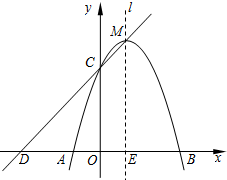 如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.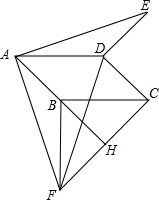 如图,在平行四边形ABCD中,∠BAD=45°.分别以BC、CD为边向外作△BCF和△DCE,使BF=BC,DE=DC,∠FBC=∠CDE,延长AB交边FC于点H,点H在F、C两点之间,连结AE、AF、DF.
如图,在平行四边形ABCD中,∠BAD=45°.分别以BC、CD为边向外作△BCF和△DCE,使BF=BC,DE=DC,∠FBC=∠CDE,延长AB交边FC于点H,点H在F、C两点之间,连结AE、AF、DF.