题目内容
9.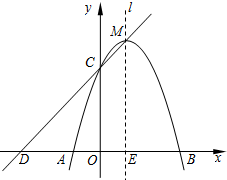 如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;
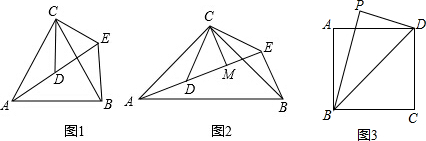
(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线l的对称点为N,试证明四边形CDAN是平行四边形;
(3)点P在直线l上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.
分析 (1)将A、C两点坐标代入解析式即可求出a、c,将解析式配成顶点式即可得到对称轴方程和顶点坐标;
(2)先由C、M两点坐标求出直线CM解析式,进而求出D点坐标,由于C、N两点关于抛物线对称轴对称,则CN∥AD,同时可求出N点坐标,然后得出CN=AD,结论显然;
(3)设出P点纵坐标,表示出MP的长度,过点P作PH⊥DM于H,表示出PH的长度,在直角三角形PAE中用勾股定理列出方程,解之即得答案.
解答 解:(1)∵抛物线y=ax2+2x+c经过点A(-1,0)和点C(0,3),
∴$\left\{\begin{array}{l}{a-2+c=0}\\{c=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-1}\\{c=3}\end{array}\right.$,
∴y=-x2+2x+3=-(x-1)2+4,
对称轴为直线x=1,顶点M(1,4);
(2)如图1,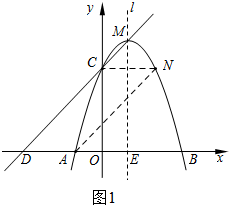
∵点C关于直线l的对称点为N,
∴N(2,3),
∵直线y=kx+b经过C、M两点,
∴$\left\{\begin{array}{l}{b=3}\\{k+b=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴y=x+3,
∵y=x+3与x轴交于点D,
∴D(-3,0),
∴AD=2=CN
又∵AD∥CN,
∴CDAN是平行四边形;
(3)设P(1,a),过点P作PH⊥DM于H,连接PA、PB,如图2,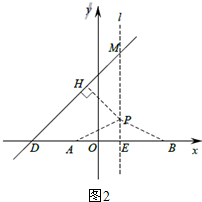
则MP=4-a,
又∠HMP=45°,
∴HP=AP=$\frac{4-a}{\sqrt{2}}$,
Rt△APE中,AP2=AE2+PE2,
即:$(\frac{4-a}{\sqrt{2}})^{2}={a}^{2}+4$,解得:$\left\{\begin{array}{l}{{a}_{1}=-4+2\sqrt{6}}\\{{a}_{2}=-4-2\sqrt{6}}\end{array}\right.$,
∴P1(1,-4+2$\sqrt{6}$),P2(1,-4-2$\sqrt{6}$).
点评 本题是二次函数综合题,主要考查了待定系数法求二次函数与一次函数解析式、求抛物线的对称轴及顶点坐标、平行四边形的判定与性质、等腰直角三角形的性质、圆的切线性质、勾股定理、解一元二次方程等知识点,综合性较强,难度适中.第(3)问的直线与圆相切问题往往转化为点到直线的距离与半径相等来解决.

| A. | 6,4 | B. | -8,14 | C. | -6,6 | D. | -8,-14 |
| A. | 互为对顶角的两角的平分线 | |
| B. | 两直线相交成的四角中相邻两角的角平分线 | |
| C. | 互为补角的两角的平分线 | |
| D. | 相邻两角的角平分线 |
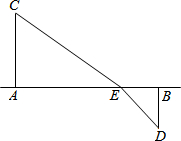 如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时
如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时
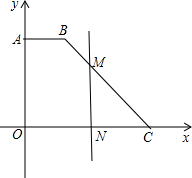 已知A(0,4)、B(2,4)、C(6,0),点M是折线A-B-C上的一个动点,MN⊥x轴于N,设ON的长为x,△MOC的面积是S,写出S与x之间的函数关系式?
已知A(0,4)、B(2,4)、C(6,0),点M是折线A-B-C上的一个动点,MN⊥x轴于N,设ON的长为x,△MOC的面积是S,写出S与x之间的函数关系式?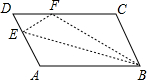 如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为6.
如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为6.