题目内容
13.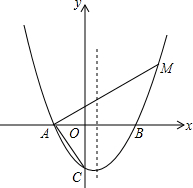 已知抛物线y=$\frac{1}{a}{x}^{2}+(\frac{2}{a}-1)x-2$(a>0)与x轴交于A、B,与y轴相交于点C,且点A在点B的左侧.
已知抛物线y=$\frac{1}{a}{x}^{2}+(\frac{2}{a}-1)x-2$(a>0)与x轴交于A、B,与y轴相交于点C,且点A在点B的左侧.(1)若抛物线过点D(2,-2),求实数a的值.
(2)在(1)的条件下,在抛物线的对称轴上找一点E,使AE+CE最小,求出点E的坐标.
(3)在第一象限内,抛物线上是否存在点M,使得以A、B、M为顶点的三角形与△ACB相似?若存在,求出a的值,若不存在,请说明理由.
分析 (1)将点D坐标代入抛物线解析式中即可;
(2)用两点之间线段最短,确定出AE+CE最小时,点E的位置即可;
(3)分两种情况同理计算,当∠MAB=∠ABC时,△ABM∽△BCA,由kAM=kBC,建立方程得出M(a+2,2+$\frac{8}{a}$),
再由相似三角形得出比例式建立方程求解即可;当∠MAB=∠BAC时,即:△ABM∽△ACB,由kAC•kAM=-1,
得出M(2a,2a+2),再用相似三角形得出的比例式建立方程求解即可.
解答 解:(1)∵抛物线过点D(2,-2),
∴$\frac{1}{a}$×4+($\frac{2}{a}$-1)×2-2=-2,
∴a=4,
(2)如图1,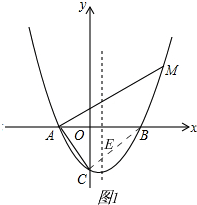
∵点A,B是抛物线与x轴的交点,
∴点B是点A关于抛物线对称轴的对称点,
∴连接BC交对称轴于点E,
∵a=4,
抛物线解析式为y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2,
∴点C(0,-2),B(4,0),对称轴x=1,
∴CB解析式为y=$\frac{1}{2}$x-2,
∴E(1,-$\frac{3}{2}$);
(3)如图2,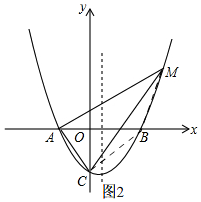
由(2)有,抛物线解析式为y=$\frac{1}{a}{x}^{2}+(\frac{2}{a}-1)x-2$=$\frac{1}{a}$(x+2)(x-a),
∴A(-2,0),B(a,0),C(0,-2),
∴AB=a+2,AC=2$\sqrt{2}$,BC=$\sqrt{{a}^{2}+4}$,
设M(m,$\frac{1}{a}$(m-a)(m+2));
①当∠MAB=∠ABC时,△ABM∽△BCA,
∴kAM=kBC,
∴$\frac{\frac{1}{a}(m-a)(m+2)}{m+2}=\frac{2}{a}$,
∴m=a+2,
∴M(a+2,2+$\frac{8}{a}$),
∵△ABM∽△BCA,
∴$\frac{AB}{BC}=\frac{BM}{AC}$,
∴$\frac{\sqrt{(a+2)^{2}}}{\sqrt{{a}^{2}+4}}=\frac{\sqrt{4+(2+\frac{8}{a})^{2}}}{2\sqrt{2}}$,
∴$\frac{4}{{a}^{2}}+\frac{2}{a}+1=0$,
∴a2+2a+4=0,
∵△=4-16<0,
∴此方程无解,
∴此种情况不存在;
②当∠MAB=∠BAC时,即:△ABM∽△ACB,
∵A(-2,0),C(0,-2),
∴∠BAC=45°,直线AC解析式为y=-x-2,
∴AC⊥AM,
∴kAC•kAM=-1,
∵kAC=-1,
∴kAM=1,
∴$\frac{\frac{1}{a}(m-a)(m+2)}{m+2}=1$,
∴m=2a,
∴M(2a,2a+2),
∵△ABM∽△ACB,
∴$\frac{AB}{AC}=\frac{AM}{AB}$,
∴AB2=AC•AM,
∴(a+2)2=2$\sqrt{2}$×$\sqrt{(2a+2)^{2}+(2a+2)^{2}}$=4(2a+2),
∴a2-4a-4=0,
∴a=2+2$\sqrt{2}$或a=2-2$\sqrt{2}$(由于点M在第一象限,所以舍去)
综合上述,a=2+2$\sqrt{2}$.
点评 此题是二次函数的综合题,主要考查待定系数法确定解析式,函数中的最值问题,点的存在问题,确定出函数解析式是解本题的关键,点的存在问题的分析是本题的难点.计算量比较大.

 阅读快车系列答案
阅读快车系列答案| A. | 在2与3之间 | B. | 在3与4之间 | C. | 在4与5之间 | D. | 在5与6之间 |
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{y}^{2}-1=0}\\{x-2y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-2x=1}\\{y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{x}+3y=0}\\{x-y=1}\end{array}\right.$ |
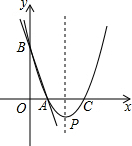 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.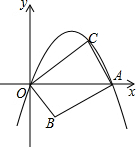 如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.
如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.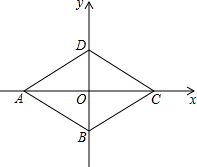 如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(-3,0)、B(0,-1)、C(3,0)、D(0,1).求证:四边形ABCD是菱形.
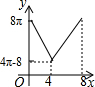
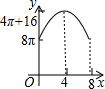
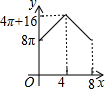
如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(-3,0)、B(0,-1)、C(3,0)、D(0,1).求证:四边形ABCD是菱形.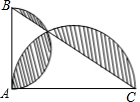 如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )
如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )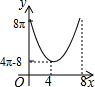
 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.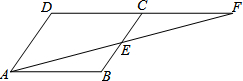 如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.
如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.