题目内容
1.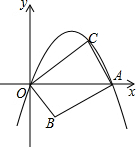 如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.
如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.(1)求点A的横坐标.(用含m的代数式表示).
(2)若m=3,则点C的坐标为(2,2).
(3)当点C与抛物线的顶点重合时,求四边形ABOC的面积.
(4)结合m的取值范围,直接写出∠AOC的度数.
分析 (1)令y=0,解方程即可.
(2)如图1中,只要证明△ADB≌△CEA即可解决问题.
(3)如图2中,由△ADB≌△CEA可得点C坐标,再利用抛物线顶点坐标公式列出方程即可解决问题.
(4)分两种情形:①O<m<1,②m>1,画出图形构造全等三角形即可解决问题.
解答 解:(1)∵抛物线y=-x2+mx与x轴交于点A,
∴-x2+mx=0,解得x=0或m,
∴点A的横坐标为m.
(2)如图1中,∵m=3,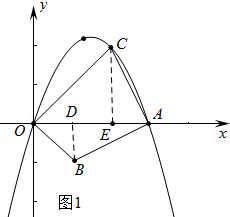
∴点A坐标为(3,0),
作BD⊥OA于D,CE⊥OA于E.
∵∠ADB=∠AEC=∠BAC=90°,
∴∠DAB+∠DBA=90°,∠DAB+∠CAE=90°,
∴∠CAE=∠DBA,
在△ADB和△CEA中,
$\left\{\begin{array}{l}{∠CAE=∠DBA}\\{∠CEA=∠BDA}\\{AC=AB}\end{array}\right.$,
∴△ADB≌△CEA,
∴BD=AE=1,AD=CE=2,
∴点C坐标(2,2).
(3)如图2中,作BD⊥OA于D,CE⊥OA于E.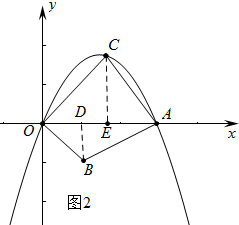
由(2)可知△ADB≌△CEA,
∴BD=AE,AD=CE
∵B(1,-1),A(m,0),
∴OE=m-1,CE=m-1,
∴C(m-1,m-1),
∵点C(m-1,m-1)与抛物线的顶点($\frac{m}{2}$,$\frac{{m}^{2}}{4}$)重合,
∴m-1=$\frac{m}{2}$,
∴m=2.
∴S四边形ABOC=$\frac{1}{2}$×2×(1+1)=2.
(4)①如图3中,当O<m<1时,∠AOC=135°,理由如下: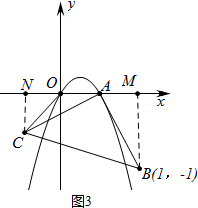
作CN⊥x轴于N,BM⊥x轴于M.
∵∠NAC+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠NAC=∠ABM,
在△ACN和△BAM中,
$\left\{\begin{array}{l}{∠NAC=∠ABM}\\{∠CNA=∠AMB}\\{AC=AB}\end{array}\right.$,
∴△ACN≌△BAM,
∴BM=AN=1,CN=AM,
∴AN=OM=1,
∴ON=CN,
∴∠NOC=∠NC0=45°,
∴∠AOC=135°
②当m>1时,∠AOC=45°,理由如下: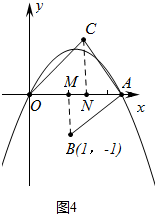
作CN⊥x轴于N,BM⊥x轴于M,∵△ACN≌△BAM,
∴BM=AN=OM=1,AM=CN,
∴ON=AM=CN,∵∠ONC=90°,
∴∠COA=45°.
点评 本题考查二次函数综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,添加辅助线构造全等三角形是解决问题的关键,学会分类讨论,需要之前画出图形,属于中考压轴题.

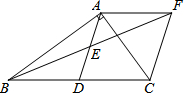 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.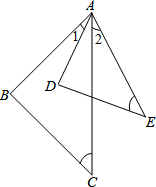 如图,△ABC与△ADE中,∠C=∠E,∠1=∠2;
如图,△ABC与△ADE中,∠C=∠E,∠1=∠2;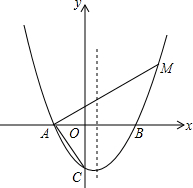 已知抛物线y=$\frac{1}{a}{x}^{2}+(\frac{2}{a}-1)x-2$(a>0)与x轴交于A、B,与y轴相交于点C,且点A在点B的左侧.
已知抛物线y=$\frac{1}{a}{x}^{2}+(\frac{2}{a}-1)x-2$(a>0)与x轴交于A、B,与y轴相交于点C,且点A在点B的左侧.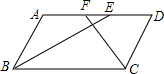 如图,在?ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F,AB=3,AD=5,则EF的长为1.
如图,在?ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F,AB=3,AD=5,则EF的长为1.