题目内容
10.甲、乙两袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标数值分别为0、-1、3,乙袋中的三张卡片上所标数值分别为-5、2、7,各任取一张卡片,并将它们的数字分别记为m、n.(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定这样一个游戏规则:若选出的m、n能使得方程x2+mx+n=0有实根,则称甲胜;否则称乙胜.请问这样的游戏规则公平吗?请你用概率知识解释.
分析 (1)首先根据题意画出树状图,然后根据树状图即可求得所有等可能的结果;
(2)利用一元二次方程根的判别式,即可判定各种情况下根的情况,然后利用概率公式求解即可求得甲、乙获胜的概率,比较概率大小,即可确定这样的游戏规是否公平.
解答 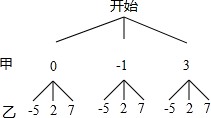 解:(1)画树状图得:
解:(1)画树状图得:
∵(m,n)的可能结果有(0,-5)、(0,7)、(0,2)、(-1,-5)、(-1,7)、(-1,2)、(3,-5)、(3,2)及(3,7),
∴(m,n)取值结果共有9种;
(2)∵(m,n)的可能结果有(0,-5)、(0,7)、(0,2)、(-1,-5)、(-1,7)、(-1,2)、(3,-5)、
(3,2)及(3,7),
∴当m=0,n=-5时,△=b2-4ac=20>0,此时x2+mx+n=0有两个不相等的实数根,
当m=0,n=7时,△=b2-4ac=-28<0,此时x2+mx+n=0没有实数根,
当m=0,n=2时,△=b2-4ac=-8<0,此时x2+mx+n=0没有实数根,
当m=-1,n=-5时,△=b2-4ac=21>0,此时x2+mx+n=0有两个不相等的实数根,
当m=-1,n=7时,△=b2-4ac=-27<0,此时x2+mx+n=0没有实数根,
当m=-1,n=2时,△=b2-4ac=-7<0,此时x2+mx+n=0没有实数根,
当m=3,n=-5时,△=b2-4ac=29>0,此时x2+mx+n=0有两个不相等的实数根,
当m=3,n=7时,△=b2-4ac=-19<0,此时x2+mx+n=0没有实数根,
当m=3,n=2时,△=b2-4ac=1>0,此时x2+mx+n=0有两个不相等的实数根,
∴P(甲获胜)=P(△≥0)=$\frac{4}{9}$,P(乙获胜)=1-$\frac{4}{9}$=$\frac{5}{9}$,
∴P(甲获胜)<P(乙获胜),
∴这样的游戏规则对乙有利,不公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

 已知一次函数y=kx+b和y=x+a的图象交于点A,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{kx-y=-b}\\{x-y=-a}\end{array}\right.$的解为( )
已知一次函数y=kx+b和y=x+a的图象交于点A,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{kx-y=-b}\\{x-y=-a}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
 青岛市确定了“拥湾发展,环湾保护”的发展战略.某中学为了让学生了解环保知识,增强环保意识,举行了一次“保护胶州湾”的环保知识竞赛.共有2000名学生参加了这次竞赛,为了解本次竞赛的情况,从中抽取了部分同学的成绩作为样本进行统计.
青岛市确定了“拥湾发展,环湾保护”的发展战略.某中学为了让学生了解环保知识,增强环保意识,举行了一次“保护胶州湾”的环保知识竞赛.共有2000名学生参加了这次竞赛,为了解本次竞赛的情况,从中抽取了部分同学的成绩作为样本进行统计.| 分组 | 频数 | 频率 |
| A组:50.5~60.5 | 16 | 0.08 |
| B组:60.5~70.5 | 0.16 | |
| C组:70.5~80.5 | 40 | 0.20 |
| D组:80.5~90.5 | 64 | 0.32 |
| E组:90.5~100 | 48 | |
| 合计 | 1 |
请根据上表和图解答下列问题:
(1)填充频率分布表中的空格并补全频数分布直方图;
(2)样本中,竞赛成绩的中位数落在D组内 (从A、B、C、D、E中选择一个正确答案);
(3)若成绩在90分以上(不含90分)获得一等奖,成绩在80分至90分之间(不含80分,含90分)获得二等奖,除此之外没有其它奖项,则本次竞赛中此中学共有多少名学生获奖?
| A. | y<-2,y>2 | B. | y<-1,y>7 | C. | -2<y<2 | D. | -1<y<7 |

