Question

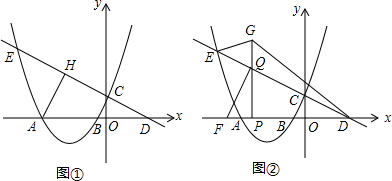
15．如图①，在Rt△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点D从点B出发，以1cm/s的速度沿BC向点C运动（不与点B，C重合），过点D作DE⊥BC交AB于点E，将△BDE沿直线DE翻折，点B落在射线BC上的点F处，N为AB的中点，过点N分别作NM⊥BC于点M，NQ⊥AC于点Q，设点D的运动时间为t（s）．
（1）直线用含t的代数式表示线段FC的长；
（2）当EF经过点Q时，求t的值；
（3）设△DEF与矩形CMNQ重叠部分的面积为S（S＞0），求S与t的函数关系式；
（4）当点D开始运动时，点P从点A出发（如图②），以2m/s的速度沿A-C-B的方向运动，当点P与点F重合时，点P与点D同时停止运动，连接NP，将△ANP沿直线NP翻折得到△NPA′，当NA′与△DEF的一边平行时，直接写出t的值．

Answer 1

分析 （1）因为点F在线段BC上或在BC的延长线上，且FC=|BC-BF|，BF=2BD由此可解；
（2）利用同角三角函数列比例式求解；
（3）①当0＜t≤4时，重叠部分的图形的面积为0；②当4＜t≤8时，如图④，重叠部分的图形为三角形，利用同角三角函数列比例式求PM、FM的值，代入面积公式化简；③如图⑥，当8＜t≤12时，重叠部分是五边形PDCHG，利用差求面积；④当12＜t＜16时，如图⑦，重叠部分的图形为矩形，直接求即可；
（4）分NA′与EF、ED、DF三边分别平行三种情况进行讨论，分别利用勾股定理列式求解．

解答 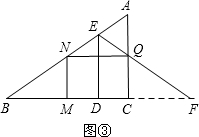解：（1）如图①，当点F在BC上时，BF=2BD=2t，则 FC=BC-BF，即 FC=16-2t    （0＜t＜8）；
 如图③，当点F在BC的延长线上时，FC=BF-BC，
即FC=2t-16  （8＜t＜16）；
（2）当EF经过点Q时，如图⑤，FC=2t-16，
∵tan∠B=tan∠EFD，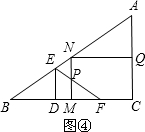
∴$\frac{AC}{BC}=\frac{CQ}{CF}$，即$\frac{12}{16}=\frac{6}{2t-16}$，t=12；
（3）由题意得：BD=t，
①当0＜t≤4时，S=0；
②当4＜t≤8时，如图④，FC=16-2t，
∴MF=8-（16-2t）=2t-8，
∵tan∠B=tan∠PFM，
∴$\frac{AC}{BC}=\frac{MP}{MF}$，即$\frac{12}{16}=\frac{MP}{2t-8}$，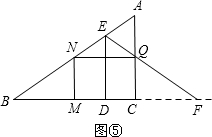
∴MP=$\frac{3（t-4）}{2}$，
∴S=S_△MPF=$\frac{1}{2}$×MP×MF=$\frac{1}{2}$（2t-8）•$\frac{3（t-4）}{2}$=$\frac{3}{2}$（t-4）²；
③如图⑥，当8＜t≤12时，重叠部分是五边形PDCHG，
FC=2t-16，
$\frac{12}{16}=\frac{CH}{2t-16}$，CH=$\frac{3（t-8）}{2}$，
同理：PG=t-8，
∵ED∥AC，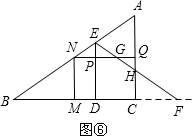
∴$\frac{ED}{12}=\frac{t}{16}$，ED=$\frac{3t}{4}$，
∴EP=$\frac{3t}{4}$-6，
∴S=S_△DEF-S_△EPG-S_△HCF，
S=$\frac{1}{2}$t•$\frac{3t}{4}$-$\frac{1}{2}$（t-8）（$\frac{3t}{4}$-6）-$\frac{1}{2}$（2t-16）•$\frac{3（t-8）}{2}$=-$\frac{3}{2}{t}^{2}+30t-120$；
④当12＜t＜16时，如图⑦，DC=16-t，
∴S=S_矩形PDCQ=DC•CQ=6（16-t）=-6t+96；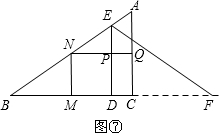
（4）分三种情况：①当A′N∥EF时，如图8，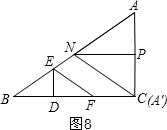

点A′与点C重合
则AP=PC=2t
∴4t=12，t=3；
②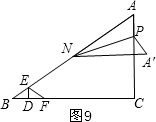当A′N∥DF时，如图9，AP=A′P=2t，
NG=8，A′G=10-8=2，AG=6，
∴A′P²=GP²+A′G²，
∴（2t）²=（6-2t）²+2²，
t=$\frac{5}{3}$；
③当A′N∥DE时，过P作PH⊥A′N于H，过N作NG⊥AC于G，
PH=NG=8，AG=6，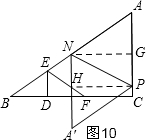
则NH=PG=2t-6，
∴A′H=10-（2t-6）=16-2t，
在Rt△A′HP中，A′P²=A′H²+HP²，
（2t）²=（16-2t）²+8²，
t=5．
综上所述，t=3或$\frac{5}{3}$或5．

点评 本题是四边形的综合题，考查了直角三角形性质和等腰直角三角形平移的问题，从一个动点的运动到两个动点，并根据翻折的性质解决问题；同时在求边的长度时，利用同角三角函数也可以求边长或表示边长，比利用相似或勾股定理简单；