题目内容
19．若抛物线y=2x2+kx-2与x轴有一个交点坐标是（1+$\sqrt{2}$，0），则k=-4，与x轴另一个交点坐标是（1-$\sqrt{2}$，0）．分析 把点（1+$\sqrt{2}$，0）代入抛物线解析式y=2x2+kx-2求出k，再令y=0解方程即可解决．
解答 解：∵抛物线y=2x2+kx-2与x轴有一个交点坐标是（1+$\sqrt{2}$，0），
∴0=2（1+$\sqrt{2}$）2+（1+$\sqrt{2}$）k-2，
∴k=-4，
∴抛物线为y=2x2-4x-2，
令y=0则2x2-4x-2=0，
x=1$±\sqrt{2}$，
∴抛物线与x轴的另一个交点为（1-$\sqrt{2}$，0）．
故答案为-4，（1-$\sqrt{2}$，0）．
点评 本题考查抛物线与x轴交点问题、待定系数法等知识，解题的关键是熟练掌握待定系数法确定函数解析式，学会求抛物线与坐标轴的交点坐标，属于中考常考题型．
练习册系列答案
相关题目
7．
正方形ABCD，正方形CEFG如图放置，点B、C、E在同一条直线上，点P在BC边上，PA=PF，且∠APF=90°，连接AF交CD于点M．有下列结论：①EC=BP；②AP=AM：③∠BAP=∠GFP；④AB2+CE2=$\frac{1}{2}$AF2；⑤S正方形ABCD+S正方形CGFE=2S△APF，其中正确的是（ ）
正方形ABCD，正方形CEFG如图放置，点B、C、E在同一条直线上，点P在BC边上，PA=PF，且∠APF=90°，连接AF交CD于点M．有下列结论：①EC=BP；②AP=AM：③∠BAP=∠GFP；④AB2+CE2=$\frac{1}{2}$AF2；⑤S正方形ABCD+S正方形CGFE=2S△APF，其中正确的是（ ）| A． | ①②③ | B． | ①③④ | C． | ①②④⑤ | D． | ①③④⑤ |
如图，直线AB∥CD，直线EF分别交直线AB、CD于点E、F、FH平分∠EFD、∠FEB=100°，则∠EHF=40°．
11．
如果实数a，b在数轴上如图所示，化简$\sqrt{{{（2-a）}^2}}-\sqrt{{{（a-3）}^2}}$的结果为（ ）
如果实数a，b在数轴上如图所示，化简$\sqrt{{{（2-a）}^2}}-\sqrt{{{（a-3）}^2}}$的结果为（ ）| A． | 5 | B． | 1 | C． | -2a+5 | D． | 2a-5 |
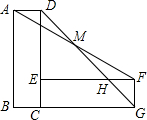如图所示，长方形ABCD绕点C顺时针旋转90°后得到长方形CEFG，连接DG交EF于H连接AF交DG于点M，若AB=4，BC=1，则AM=$\frac{\sqrt{34}}{2}$．