题目内容
 如图所示,△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,有以下四个结论:
如图所示,△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,有以下四个结论:①∠PBC=∠PCB=15°;②AD∥BC;③直线PC与AB垂直;④四边形ABCD是轴对称图形.
其中正确结论有
考点:等边三角形的性质,全等三角形的判定与性质,轴对称图形
专题:
分析:根据等边三角形和全等三角形的性质得出∠PAB=∠APB=∠PBA=∠PDC=∠PCD=∠DPC=60°,AB=DC,PB=PC,PA=PD,∠APD=90°,再逐个求出即可.
解答: 解:延长CP交AB于M,
解:延长CP交AB于M,
∵△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,
∴∠PAB=∠APB=∠PBA=∠PDC=∠PCD=∠DPC=60°,AB=DC,PB=PC,PA=PD,∠APD=90°,
∴∠BPC=380°-90°-60°-60°=150°,∠PAD=∠PDA=45°,
∵PB=PC,
∴∠PBC=∠PCB=15°,
∴∠DAB+∠ABC=45°+60°+60°+15°=180°,
∴AD∥BC,
∵∠CMB=180°-15°-15°-60°=90°,
∴CP⊥AB,
∵AD∥BC,AB=CD,
∴四边形ABCD是等腰梯形,
∴四边形ABCD是轴对称图形,
∴①②③④都正确,
故答案为:4.
 解:延长CP交AB于M,
解:延长CP交AB于M,∵△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,
∴∠PAB=∠APB=∠PBA=∠PDC=∠PCD=∠DPC=60°,AB=DC,PB=PC,PA=PD,∠APD=90°,
∴∠BPC=380°-90°-60°-60°=150°,∠PAD=∠PDA=45°,
∵PB=PC,
∴∠PBC=∠PCB=15°,
∴∠DAB+∠ABC=45°+60°+60°+15°=180°,
∴AD∥BC,
∵∠CMB=180°-15°-15°-60°=90°,
∴CP⊥AB,
∵AD∥BC,AB=CD,
∴四边形ABCD是等腰梯形,
∴四边形ABCD是轴对称图形,
∴①②③④都正确,
故答案为:4.
点评:本题考查了等腰梯形的性质和判定,平行线的判定,全等三角形的性质,等边三角形的性质的应用,主要考查学生的推理能力,综合性比较强,有一定的难度.

练习册系列答案
相关题目
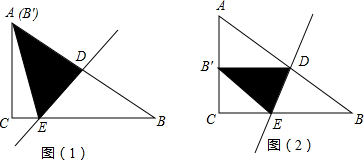
 如图,AC∥EF∥BD.
如图,AC∥EF∥BD. 如图,圆的两弦的延长线交圆外于点P,若PC=4,CD=3,A为PB中点,求PB的长.
如图,圆的两弦的延长线交圆外于点P,若PC=4,CD=3,A为PB中点,求PB的长.