题目内容
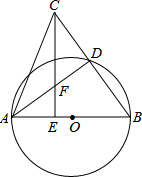
如图，圆的两弦的延长线交圆外于点P，若PC=4，CD=3，A为PB中点，求PB的长．考点：切割线定理
专题：
分析：求出PD，根据圆内接四边形的性质求出∠PAC=∠D，证△PAC∽△PDB，根据相似得出比例式，代入求出x即可．
解答：解：∵PC=4，CD=3，
∴PD=4+3=7，
∵A为PB中点，
∴PA=AB，
设PA=AB=x，则PB=2x，
如图，连接AC、BD，
∵A、B、D、C四点共圆，
∴∠PAC=∠D，
∵∠P=∠P，
∴△PAC∽△PDB，
∴
=
，
∴
=
，
解得：x=
，
∴PB=2x=2
．
∴PD=4+3=7，
∵A为PB中点，
∴PA=AB，
设PA=AB=x，则PB=2x，
如图，连接AC、BD，
∵A、B、D、C四点共圆，
∴∠PAC=∠D，
∵∠P=∠P，
∴△PAC∽△PDB，
∴
| PA |
| PD |
| PC |
| PB |
∴
| x |
| 7 |
| 4 |
| 2x |
解得：x=
| 14 |
∴PB=2x=2
| 14 |
点评：本题考查了圆内接四边形的性质，相似三角形的性质和判定的应用，解此题的关键是得出比例式，题目比较好，难度适中．
练习册系列答案
相关题目
如图所示，在△ABC中，AB=AC，AE=
如图，已知直角扇形AOB的半径OA=2cm，以OB为直径在扇形内作半圆M，过点M引MP∥AO交
如图所示，△ABP和△CDP是两个全等的等边三角形，且AP⊥PD，有以下四个结论：已知某矩形的两邻边的边长比为1：2，若以较长一边为直径作半圆，则该矩形的各边与半圆相切的线段有（ ）
| A、0条 | B、1条 | C、2条 | D、3条 |
已知：AB=AC，O为BC中点，⊙O与AB边相切于点D．求证：⊙O与AC边相切．