题目内容
式子（1+
）•（1+
）•（1+
）•（1+
）•（1+
）•（1+
）•（1+
）•（1+
）•（1+
）•（1+
）•（1+
）…第n项为 ．
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| 4×6 |
| 1 |
| 5×7 |
| 1 |
| 6×8 |
| 1 |
| 7×9 |
| 1 |
| 8×10 |
| 1 |
| 9×11 |
| 1 |
| 10×12 |
| 1 |
| 11×13 |
考点：规律型：数字的变化类
专题：规律型
分析：观察所给的几项数，得到每项由整数部分和分数部分组成，整数部分都是1，而分数部分的分子为1，分母中的第1个因数等于序号数，另一个因数比序号数大2，由此得到所以第n项为1+
．
| 1 |
| n(n+2) |
解答：解：第1项为1+
，
第2项为1+
，
第3项为1+
第4项为1+
，
…
所以第n项为1+
．
故答案为1+
．
| 1 |
| 1×3 |
第2项为1+
| 1 |
| 2×4 |
第3项为1+
| 1 |
| 3×5 |
第4项为1+
| 1 |
| 4×6 |
…
所以第n项为1+
| 1 |
| n(n+2) |
故答案为1+
| 1 |
| n(n+2) |
点评：本题考查了规律型-数字的变化类：通过特殊数字的变化情况找出其中不变的因素，然后进行推广得到一般的变化规律．
练习册系列答案
相关题目
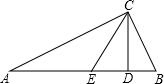在△ABC中，∠ACB=90°，CD、CE三等分∠ACB，CD⊥AB，求证：CE=AE=EB．
如图所示，△ABP和△CDP是两个全等的等边三角形，且AP⊥PD，有以下四个结论：