题目内容
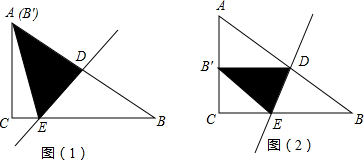
在△ABC中,AC=6,BC=8,AB=10,D、E分别是边AB、边BC上的点,把△ABC沿着直线DE对折,顶点B的对应点是点B′:
(1)如图(1),如果点B′和顶点A重合,求CE的长;
(2)如图(2),如果点B′落在AC的中点,求CE的长.
(1)如图(1),如果点B′和顶点A重合,求CE的长;
(2)如图(2),如果点B′落在AC的中点,求CE的长.

考点:翻折变换(折叠问题)
专题:
分析:(1)如图1,证明∠C=90°;设CE=λ,则BE=8-λ;根据勾股定理列出关于λ的方程,解方程即可解决问题.
(2)如图2,首先求出CB′=3;类比(1)中的解法,设出未知数,列出方程即可解决问题.
(2)如图2,首先求出CB′=3;类比(1)中的解法,设出未知数,列出方程即可解决问题.
解答: 解:(1)如图1,
解:(1)如图1,
∵AC=6,BC=8,AB=10,且62+82=102,
∴∠C=90°,设CE=λ,则BE=8-λ;
由题意得:AE=BE=8-λ,
由勾股定理得:λ2=62+(8-λ)2,
解得:λ=
,
即CE的长为
.
(2)如图2,
∵点B′落在AC的中点,
∴CB′=
AC=3;
设CE=λ,类比(1)中的解法,可列出方程:
λ2+32=(8-λ)2
解得:λ=
.
即CE的长为
.
 解:(1)如图1,
解:(1)如图1,∵AC=6,BC=8,AB=10,且62+82=102,
∴∠C=90°,设CE=λ,则BE=8-λ;
由题意得:AE=BE=8-λ,
由勾股定理得:λ2=62+(8-λ)2,
解得:λ=
| 25 |
| 4 |
即CE的长为
| 25 |
| 4 |
(2)如图2,
∵点B′落在AC的中点,
∴CB′=
| 1 |
| 2 |
设CE=λ,类比(1)中的解法,可列出方程:
λ2+32=(8-λ)2
解得:λ=
| 55 |
| 16 |
即CE的长为
| 55 |
| 16 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用翻折变换的性质,找出图形中隐含的等量关系;借助勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,∠FDE=∠B,BD=2,CD=3,CE=4,AE=1,那么AF的长为( )
如图,已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,∠FDE=∠B,BD=2,CD=3,CE=4,AE=1,那么AF的长为( ) 勐海茶树王是西双版内众多古树之一,至今已有1800年的历史,茶树王于2012年10月“仙逝”.小刚曾经通过测量计算过茶树王的高度,他测量的方法是:如图,从点B沿水平线方向走到点D测得BD=17m,再用高为1.5m的测角仪CD,测得树顶的仰角为60°.请你根据以上数据计算茶树王AB的高度.(结果保留整数,
勐海茶树王是西双版内众多古树之一,至今已有1800年的历史,茶树王于2012年10月“仙逝”.小刚曾经通过测量计算过茶树王的高度,他测量的方法是:如图,从点B沿水平线方向走到点D测得BD=17m,再用高为1.5m的测角仪CD,测得树顶的仰角为60°.请你根据以上数据计算茶树王AB的高度.(结果保留整数, 如图所示,在△ABC中,AB=AC,AE=
如图所示,在△ABC中,AB=AC,AE= 如图所示,△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,有以下四个结论:
如图所示,△ABP和△CDP是两个全等的等边三角形,且AP⊥PD,有以下四个结论: