题目内容
5.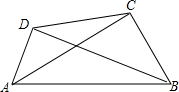 如图,∠ACB=90°,AC=20.BC=15,AD=7,BD=24.
如图,∠ACB=90°,AC=20.BC=15,AD=7,BD=24.(1)求证:∠ADB=90°;
(2)求证:∠ACD=∠ABD.
分析 (1)由勾股定理求出AB,由勾股定理的逆定理证明△ABD是直角三角形即可;
(2)证明A、B、C、D四点共圆,由圆周角定理即可得出结论.
解答 (1)证明:∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2{0}^{2}+1{5}^{2}}$=25,
∵72+242=252,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,∠ADB=90°;
(2)证明:∵∠ADB=∠ACB=90°,
∴A、B、C、D四点共圆,
∴∠ACD=∠ABD.
点评 本题考查了勾股定理、勾股定理的逆定理、四点共圆、圆周角定理;熟练掌握勾股定理,由勾股定理的逆定理证明直角三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
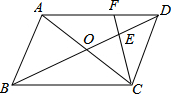 如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8.
如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8.