题目内容
20.已知直线y=x+1与两个坐标轴的交点是A、B,把y=-2x2平移后经过A、B两点,则平移后的二次函数解析式为y=-2x2-x+1.分析 先利用坐标轴上点的坐标特征确定A点坐标为(0,1),B点坐标为(-1,0),再设平移后的抛物线解析式为y=2x2+bx+c,然后把A点和B点坐标代入得到b和c的方程,再解方程组求出b、c即可得到平移的抛物线解析式.
解答 解:把x=0代入y=x+1得y=1,则A点坐标为(0,1);把y=0代入y=x+1得x+1=0,解得x=-1,则B点坐标为(-1,0),
设平移后的抛物线解析式为y=-2x2+bx+c,
把A(0,1)、B(-1,0)代入得$\left\{\begin{array}{l}{c=1}\\{-2-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-1}\\{c=1}\end{array}\right.$,
所以平移的抛物线解析式为y=-2x2-x+1.
故答案为y=-2x2-x+1.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
10.下列各题中计算正确的是( )
| A. | 3x2-x2=2 | B. | (a3)2•a5=a30 | C. | (x2)3•x+x5•x2=2x7 | D. | (-a2)3=a6 |
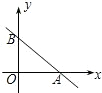 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.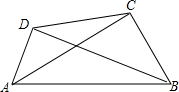 如图,∠ACB=90°,AC=20.BC=15,AD=7,BD=24.
如图,∠ACB=90°,AC=20.BC=15,AD=7,BD=24.