题目内容
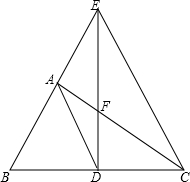 如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF.
如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF.考点:相似三角形的判定与性质
专题:证明题
分析:要证明AD2=DE•DF,只需证明△ADF∽△ADF即可.
解答:解:∵BC的垂直平分线交BC于D,
∴DA=DC,∠BAC=90°
∴∠DAC=∠DCA,
又∵∠BAC=90°,∠B+∠BED=90°,∠B+∠ACB=90°,
∴∠ACB=∠BED,
∴∠DAC=∠BED,
在△ADF和△ADE中,
,
∴△ADF∽△ADE,
∴
=
,
∴AD2=DE•DF.
∴DA=DC,∠BAC=90°
∴∠DAC=∠DCA,
又∵∠BAC=90°,∠B+∠BED=90°,∠B+∠ACB=90°,
∴∠ACB=∠BED,
∴∠DAC=∠BED,
在△ADF和△ADE中,
|
∴△ADF∽△ADE,
∴
| AD |
| DE |
| DF |
| AD |
∴AD2=DE•DF.
点评:本题考查了相似三角形的判定与性质.解答本题的关键在于注意掌握数形结合思想的应用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
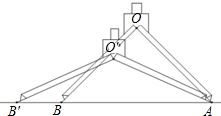 如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )
如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )A、2
| ||
B、
| ||
C、2
| ||
D、2-
|
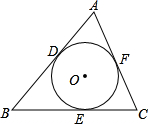 已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.
已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长. 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有 如图,AC⊥DE,垂足为O,∠B=35°,∠E=25°,求∠A的度数.
如图,AC⊥DE,垂足为O,∠B=35°,∠E=25°,求∠A的度数.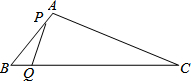 如图,在△ABC中,AB=10cm.BC=20cm、点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过几秒钟后,以P、B、Q三点为顶点的三角形与△ABC相似?
如图,在△ABC中,AB=10cm.BC=20cm、点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过几秒钟后,以P、B、Q三点为顶点的三角形与△ABC相似? 如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.