题目内容
如图，AC⊥DE，垂足为O，∠B=35°，∠E=25°，求∠A的度数．考点：三角形内角和定理
专题：
分析：先根据三角形外角的性质得出∠ADO的度数，再由直角三角形的性质即可得出结论．
解答：解：∵∠ADO是△BDE的外角，∠B=35°，∠E=25°，
∴∠ADO=∠B+∠E=35°+25°=60°．
∵AC⊥DE，垂足为O，
∴∠AOD=90°，
∴∠A=90°-∠ADO=90°-60°=30°．
∴∠ADO=∠B+∠E=35°+25°=60°．
∵AC⊥DE，垂足为O，
∴∠AOD=90°，
∴∠A=90°-∠ADO=90°-60°=30°．
点评：本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
相关题目
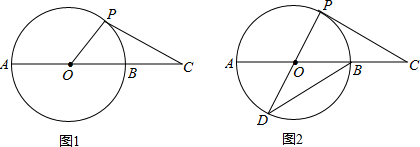
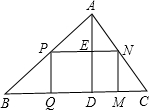如图，△ABC是一块锐角三角形材料，BC=120mm，高AD=80mm，要把它加工成一矩形零件，使矩形一边在BC上，其余两个顶点分别在AB、AC上．
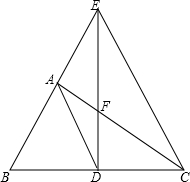如图，在△ABC中，∠BAC=90°，BC的垂直平分线交BC于D，交BA的延长线于E，交AC于F，求证：AD2=DE•DF．
已知如图，a∥b，且∠1=100°，则∠3=