题目内容
已知实数a，b分别满足a2-6a+4=0，b2-6b+4=0，且a≠b，求
+
的值．
| b |
| a |
| a |
| b |
考点：根与系数的关系
专题：计算题
分析：根据题意，a、b可看作方程x2-6x+4=0的两根，则根据根与系数的关系得到a+b=6，ab=4，然后把原式变形得到原式=
=
，再利用整体代入的方法计算即可．
| a2+b2 |
| ab |
| (a+b)2-2ab |
| ab |
解答：解：∵a2-6a+4=0，b2-6b+4=0，且a≠b，
∴a，b可看作方程x2-6x+4=0的两根，
∴a+b=6，ab=4，
∴原式=
=
=
=7．
∴a，b可看作方程x2-6x+4=0的两根，
∴a+b=6，ab=4，
∴原式=
| a2+b2 |
| ab |
| (a+b)2-2ab |
| ab |
| 62-2×4 |
| 4 |
点评：本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-
，x1x2=
．
| b |
| a |
| c |
| a |
练习册系列答案
相关题目
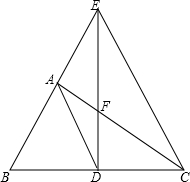如图，在△ABC中，∠BAC=90°，BC的垂直平分线交BC于D，交BA的延长线于E，交AC于F，求证：AD2=DE•DF．
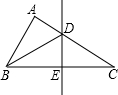如图，在△ABC中，BC边上的垂直平分线交AC于点D，
已知如图，a∥b，且∠1=100°，则∠3=
为了方便学生安全出行，我市推出了学生公交专线．某校对学生出行情况作简要调查后，初步整理了一份信息（如图）．根据信息，解答下列问题．