题目内容
 如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.(1)画出旋转后的△A1B1C;
(2)求△ABC在旋转过程中所扫过部分的面积.
考点:作图-旋转变换,扇形面积的计算
专题:作图题
分析:(1)根据网格结构找出点A、B绕着点C顺时针旋转90°后的对应点A1、B1的位置,然后与点C顺次连接即可;
(2)根据扫过的面积等于扇形的面积与三角形的面积的和列式计算即可得解.
(2)根据扫过的面积等于扇形的面积与三角形的面积的和列式计算即可得解.
解答: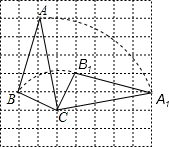 解:(1)△A1B1C如图所示;
解:(1)△A1B1C如图所示;
(2)△ABC的面积=2×5-
×1×2-
×1×5-
×1×4
=10-1-2.5-2
=10-5.5
=4.5,
由勾股定理得,AC=
=
,
所以,扫过部分的面积=
+4.5=
π+4.5.
 解:(1)△A1B1C如图所示;
解:(1)△A1B1C如图所示;(2)△ABC的面积=2×5-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=10-1-2.5-2
=10-5.5
=4.5,
由勾股定理得,AC=
| 12+52 |
| 26 |
所以,扫过部分的面积=
90•π•(
| ||
| 360 |
| 13 |
| 2 |
点评:本题考查了利用旋转变换作图,扇形的面积,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
已知圆锥的底面半径为6,侧面积为60π,则这个圆锥的母线为( )
| A、6 | B、8 | C、10 | D、12 |
 如图,在△ABC中,BC=a,AC=b,AB=c,∠C=90°,CD和BE是△ABC的两条中线,且CD⊥BE,则a:b:c=
如图,在△ABC中,BC=a,AC=b,AB=c,∠C=90°,CD和BE是△ABC的两条中线,且CD⊥BE,则a:b:c=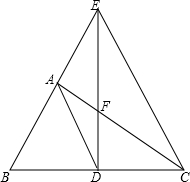 如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF.
如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF. 为了方便学生安全出行,我市推出了学生公交专线.某校对学生出行情况作简要调查后,初步整理了一份信息(如图).根据信息,解答下列问题.
为了方便学生安全出行,我市推出了学生公交专线.某校对学生出行情况作简要调查后,初步整理了一份信息(如图).根据信息,解答下列问题.