题目内容
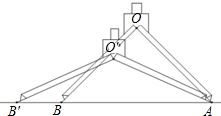 如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )
如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )A、2
| ||
B、
| ||
C、2
| ||
D、2-
|
考点:解直角三角形的应用
专题:
分析:△ABO是等腰直角三角形,利用三角函数即可求得OA的长,过O'作O'D⊥AB于点D,在直角△AO'D中利用三角函数求得AD的长,则AB'=2AD,然后根据BB'=AB'-AB即可求解.
解答: 解:在等腰直角△OAB中,AB=4,则OA=
解:在等腰直角△OAB中,AB=4,则OA=
AB=2
cm,
∠AO'D=
×120°=60°,
过O'作O'D⊥AB于点D.
则AD=AO'•sin60°=2
×
=
.
则AB'=2AD=2
,
故BB'=AB'-AB=2
-4.
故选A.
 解:在等腰直角△OAB中,AB=4,则OA=
解:在等腰直角△OAB中,AB=4,则OA=
| ||
| 2 |
| 2 |
∠AO'D=
| 1 |
| 2 |
过O'作O'D⊥AB于点D.
则AD=AO'•sin60°=2
| 2 |
| ||
| 2 |
| 6 |
则AB'=2AD=2
| 6 |
故BB'=AB'-AB=2
| 6 |
故选A.
点评:此题考查了三角函数的基本概念,主要是三角函数的概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
已知圆锥的底面半径为6,侧面积为60π,则这个圆锥的母线为( )
| A、6 | B、8 | C、10 | D、12 |
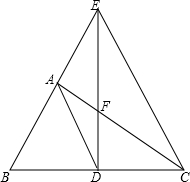 如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF.
如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF.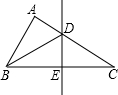 如图,在△ABC中,BC边上的垂直平分线交AC于点D,
如图,在△ABC中,BC边上的垂直平分线交AC于点D,