题目内容
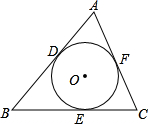 已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.
已知⊙O分别切△ABC的三边AB、BC、CA,切点D、E、F.若BC=a,AC=b,AB=c,求AD、BE、CF的长.考点:三角形的内切圆与内心
专题:
分析:根据切线长定理,设AD=x,BE=y,CF=z,则AF=AD=x,BD=BE=y,CE=CF=z,然后列方程组即可求解.
解答:解:设AD=x,BE=y,CF=z,则AF=AD=x,BD=BE=y,CE=CF=z.
根据题意得:
,
解得:
.
故AD=
,BE=
,CF=
.
根据题意得:
|
解得:
|
故AD=
| b+c-a |
| 2 |
| a+c-b |
| 2 |
| a+b-c |
| 2 |
点评:本题考查了切线长定理,正确解方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知四边形ABCD中,AB=CD,AD=CB,求证:AD∥BC.
已知四边形ABCD中,AB=CD,AD=CB,求证:AD∥BC.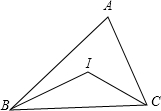 如图,在△ABC中,∠A=72°,点I是△ABC内的一点.
如图,在△ABC中,∠A=72°,点I是△ABC内的一点. 如图,在△ABC中,BC=a,AC=b,AB=c,∠C=90°,CD和BE是△ABC的两条中线,且CD⊥BE,则a:b:c=
如图,在△ABC中,BC=a,AC=b,AB=c,∠C=90°,CD和BE是△ABC的两条中线,且CD⊥BE,则a:b:c=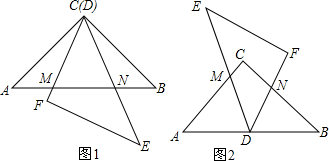
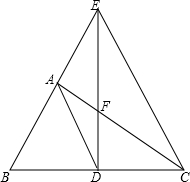 如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF.
如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交BA的延长线于E,交AC于F,求证:AD2=DE•DF.