题目内容
已知点M（2，3）在双曲线y=
上，则下列各点一定不在该双曲线上的是（ ）
| k |
| x |
| A、（3，2） |
| B、（-2，-3） |
| C、（1，6） |
| D、（3，-2） |
考点：反比例函数图象上点的坐标特征
专题：
分析：首先根据点M（2，3）在双曲线y=
上，把M（2，3）代入函数解析式可得k的值，再把四个选项中的点的坐标分别用横纵坐标相乘，即等于k的值的就在函数图象上．
| k |
| x |
解答：解：∵点M（2，3）在双曲线y=
上，
∴k=2×3=6，
A、3×2=6，故此点在双曲线上；
B、（-2）×（-3）=6，故此点在双曲线上；
C、1×6=6，故此点在双曲线上；
D、3×（-2）=-6≠6，故此点不在双曲线上；
故选：D．
| k |
| x |
∴k=2×3=6，
A、3×2=6，故此点在双曲线上；
B、（-2）×（-3）=6，故此点在双曲线上；
C、1×6=6，故此点在双曲线上；
D、3×（-2）=-6≠6，故此点不在双曲线上；
故选：D．
点评：此题主要考查了反比例函数图象上点的坐标特征，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
练习册系列答案
相关题目
已知：y=
+
+
，则代数式
-
的值为（ ）
| 1-8x |
| 8x-1 |
| 1 |
| 2 |
|
|
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |
平行四边形两邻边分别为24和16，若两长边间的距离为8，则两短边间的距离为（ ）
| A、5 | B、6 | C、8 | D、12 |
若
+|2x+y-7|=0，则x，y的值是（ ）
| x-y-2 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列每组数据表示3根小木棒的长度，其中能组成一个三角形的是（ ）
| A、3cm，4cm，7cm |
| B、3cm，4cm，6cm |
| C、5cm，4cm，10cm |
| D、5cm，3cm，8cm |
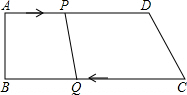如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8，AD=24，BC=32，点P从A点出发，以1cm/s的速度向D运动，点Q从C点同时出发，以3cm/s的速度向B运动，规定其中一个动点到达端点时，另一个动点，也随之停止运动．