题目内容
 如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积.
如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积.考点:平行四边形的性质,勾股定理
专题:
分析:利用平行四边形的性质得出OA,OD的长,利用勾股定理得出AD的长,再利用平行四边形面积公式求出即可.
解答:解:∵AC、BD是平行四边形ABCD的对角线,
∴OA=
AC=6,OD=
BD=3,
在Rt△ADO中,由勾股定理可得出:
AD=
=
=3
,
∴S平行四边形ABCD=AD•BD=3
×6=18
.
∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ADO中,由勾股定理可得出:
AD=
| OA2-OD2 |
| 62-32 |
| 3 |
∴S平行四边形ABCD=AD•BD=3
| 3 |
| 3 |
点评:此题主要考查了平行四边形的性质以及勾股定理等知识,得出AD的长是解题关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
若3<m<4,那么
-
的结果是( )
| (3-m)2 |
| (m-4)2 |
| A、7+2m | B、2m-7 |
| C、7-2m | D、-1-2m |
若
+|2x+y-7|=0,则x,y的值是( )
| x-y-2 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
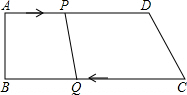 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,AD=24,BC=32,点P从A点出发,以1cm/s的速度向D运动,点Q从C点同时出发,以3cm/s的速度向B运动,规定其中一个动点到达端点时,另一个动点,也随之停止运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,AD=24,BC=32,点P从A点出发,以1cm/s的速度向D运动,点Q从C点同时出发,以3cm/s的速度向B运动,规定其中一个动点到达端点时,另一个动点,也随之停止运动. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′的度数.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′的度数.