题目内容
9.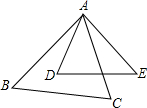 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )| A. | $\frac{AC}{AD}$=$\frac{AB}{AE}$ | B. | $\frac{AC}{AD}$=$\frac{BC}{DE}$ | C. | $\frac{AC}{AD}$=$\frac{AB}{DE}$ | D. | $\frac{AC}{AD}$=$\frac{BC}{AE}$ |
分析 本题中已知∠BAC=∠D,则对应的夹边比值相等即可使△ABC与△ADE相似,结合各选项即可得问题答案.
解答 解:∵∠BAC=∠D,$\frac{AC}{AD}=\frac{AB}{DE}$,
∴△ABC∽△ADE.
故选C.
点评 此题考查了相似三角形的判定:①有两个对应角相等的三角形相似;②有两个对应边的比相等,且其夹角相等,则两个三角形相似;③三组对应边的比相等,则两个三角形相似,熟记各种判定相似三角形的方法是解题关键.

练习册系列答案
相关题目
20.已知-x2ym+1与3xny4是同类项,则mn的值为( )
| A. | 6 | B. | 9 | C. | 8 | D. | 5 |
17.为鼓励民众节约用电,城镇居民生活用电电费目前实行梯度收费,具体标准如下表:
(1)若月用电100千瓦时,应交电费多少元?若月用电200千瓦时,应交电费多少元?
(2)若某用户12月应交电费93元,该用户12月的用电量是多少?
| 月用电量(单位:千瓦时) | 单价(单位:元) |
| 150以内(含150) | 0.5 |
| 超过150但不超过300的部分(含300) | 0.6 |
| 300以上(不含300)的部分 | 0.8 |
(2)若某用户12月应交电费93元,该用户12月的用电量是多少?
1.下列说法中错误的是( )
| A. | 篮球队员在罚球线上投篮一次,未投中是随机事件 | |
| B. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| C. | “抛一枚硬币,正面向上的概率为$\frac{1}{2}$”表示每抛两次就有一次正面朝上 | |
| D. | “抛一枚均匀的正方体骰子,朝上的点数是6的概率为$\frac{1}{6}$”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在$\frac{1}{6}$附近 |
 如图,正方形ABCD的边长为2,E是BC的中点,将△ABE绕点A顺时针旋转90°,设点E的对应点为F.
如图,正方形ABCD的边长为2,E是BC的中点,将△ABE绕点A顺时针旋转90°,设点E的对应点为F.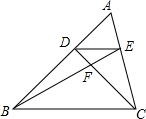 如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.
如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$. 如图,在平面直角坐标系中,四边形OABC各个顶点的坐标分别为O(0,0),A(6,0),B(4,4),C(2,3),求这个四边形OABC的面积.
如图,在平面直角坐标系中,四边形OABC各个顶点的坐标分别为O(0,0),A(6,0),B(4,4),C(2,3),求这个四边形OABC的面积.