题目内容
18．在Rt△ABC中，若两条直角边的比为7：24，则最小角的正切值为$\frac{7}{25}$．分析 设两直角边分别为7x，24x，利用勾股定理可计算出斜边为25x，然后根据正切值求解．
解答 解：∵两条直角边的比为7：24，
∴设两直角边分别为7x，24x，
∴斜边=$\sqrt{（7x）^{2}+（24x）^{2}}$=25x，
∴最小角的正切值=$\frac{7x}{25x}$=$\frac{7}{25}$．
故答案为$\frac{7}{25}$．
点评 本题考查了锐角三角函数的定义：在Rt△ABC中，∠C=90°，锐角A的对边a与斜边c的比叫做∠A的正弦，记作sinA；锐角A的邻边b与斜边c的比叫做∠A的余弦，记作cosA；锐角A的对边a与邻边b的比叫做∠A的正切，记作tanA．
练习册系列答案
相关题目
8．2014第二届中国（绵阳）科技城国际博览会科技部、国家知识产权局、国家国防科工局和四川省人民政府共同主办，于2014年10月16日至18日在中国科技城-四川省绵阳市落幕，记者从大会组委会获悉，本届科博会签约项目945个，金额达883.6亿元，把883.6亿元用科学记数法表示为（ ）
| A． | 883.6×108元 | B． | 8.836×109元 | C． | 8.836×1010元 | D． | 8.836×1011元 |
9．
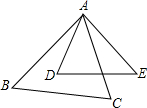如图，在△ABC与△ADE中，∠BAC=∠D，要使△ABC与△ADE相似，还需满足下列条件中的（ ）
如图，在△ABC与△ADE中，∠BAC=∠D，要使△ABC与△ADE相似，还需满足下列条件中的（ ）| A． | $\frac{AC}{AD}$=$\frac{AB}{AE}$ | B． | $\frac{AC}{AD}$=$\frac{BC}{DE}$ | C． | $\frac{AC}{AD}$=$\frac{AB}{DE}$ | D． | $\frac{AC}{AD}$=$\frac{BC}{AE}$ |
13．已知m=n，下列等式不成立的是（ ）
| A． | 3m=3n | B． | $\frac{m}{4}$=$\frac{n}{4}$ | C． | -m+2=-n+2 | D． | m+1=n-1 |