题目内容
4. 如图,正方形ABCD的边长为2,E是BC的中点,将△ABE绕点A顺时针旋转90°,设点E的对应点为F.
如图,正方形ABCD的边长为2,E是BC的中点,将△ABE绕点A顺时针旋转90°,设点E的对应点为F.(1)画出旋转后的三角形(尺规作图,保留作图痕迹,不写作法);
(2)求出点E运动到点F所经过的路径的长.
分析 (1)延长DA到G点,使AG=AB,然后分别以A、G为圆心,AE、BE为半径画弧,两弧相交于点F,则△AGF即为所作;
(2)点E运动到点F所经过的路径是以A点为圆心,AB为半径.圆心角为90°的弧,然后根据弧长公式求解.
解答 解:(1)如图,△AGF为所作;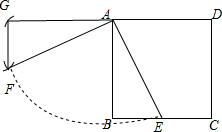
(2)∵E是BC的中点,
∴BE=1,
∴AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵△ABE绕点A顺时针旋转90°得到△AGF,
∴∠EAF=90°,
∴点E运动到点F所经过的路径的长=$\frac{90•π•\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了弧长公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列两个图形一定相似的是( )
| A. | 两个菱形 | B. | 两个矩形 | C. | 两个正方形 | D. | 两个等腰梯形 |
19.已知点A(-1,y1),B (2,y2)是反比例函数y=-$\frac{5}{x}$的图象上的两点,下列结论正确的是( )
| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
9.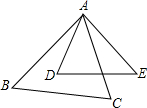 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )| A. | $\frac{AC}{AD}$=$\frac{AB}{AE}$ | B. | $\frac{AC}{AD}$=$\frac{BC}{DE}$ | C. | $\frac{AC}{AD}$=$\frac{AB}{DE}$ | D. | $\frac{AC}{AD}$=$\frac{BC}{AE}$ |
13.已知m=n,下列等式不成立的是( )
| A. | 3m=3n | B. | $\frac{m}{4}$=$\frac{n}{4}$ | C. | -m+2=-n+2 | D. | m+1=n-1 |
 如图,已知A、B、C、D四点,根据下列要求画图:
如图,已知A、B、C、D四点,根据下列要求画图: 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE=$\frac{1}{2}$.
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE=$\frac{1}{2}$.