��Ŀ����
1������˵���д�����ǣ�������| A�� | �����Ա�ڷ�������Ͷ��һ�Σ�δͶ��������¼� | |
| B�� | �����⻭��һ��ƽ���ı��Σ��������ĶԳ�ͼ�Ρ��DZ�Ȼ�¼� | |
| C�� | ����һöӲ�ң��������ϵĸ���Ϊ$\frac{1}{2}$����ʾÿ�����ξ���һ�����泯�� | |
| D�� | ����һö���ȵ����������ӣ����ϵĵ�����6�ĸ���Ϊ$\frac{1}{6}$����ʾ�����������������ӣ����׳����ϵĵ�����6����һ�¼�������Ƶ���ȶ���$\frac{1}{6}$���� |
���� ֱ����������¼��Ķ����ϸ��ʵ�����ֱ�����ó��𰸣�
��� �⣺A�������Ա�ڷ�������Ͷ��һ�Σ�δͶ��������¼�����ȷ���������⣻
B�������⻭��һ��ƽ���ı��Σ��������ĶԳ�ͼ�Ρ��DZ�Ȼ�¼�����ȷ���������⣻
C������һöӲ�ң��������ϵĸ���Ϊ$\frac{1}{2}$����ʾ�����������������ӣ����������ϡ���һ�¼�������Ƶ���ȶ���$\frac{1}{2}$��������ѡ����������⣻
D������һö���ȵ����������ӣ����ϵĵ�����6�ĸ���Ϊ$\frac{1}{6}$����ʾ�����������������ӣ����׳����ϵĵ�����6����һ�¼�������Ƶ���ȶ���$\frac{1}{6}$��������ȷ��
��ѡ��C��
���� ������Ҫ����������¼��Ķ�����ʵ����壬��ȷ������ض����ǽ���ؼ���

��ϰ��ϵ�д�
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д�
�����Ŀ
9��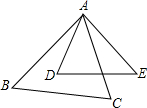 ��ͼ���ڡ�ABC���ADE�У���BAC=��D��Ҫʹ��ABC���ADE���ƣ������������������еģ�������
��ͼ���ڡ�ABC���ADE�У���BAC=��D��Ҫʹ��ABC���ADE���ƣ������������������еģ�������
 ��ͼ���ڡ�ABC���ADE�У���BAC=��D��Ҫʹ��ABC���ADE���ƣ������������������еģ�������
��ͼ���ڡ�ABC���ADE�У���BAC=��D��Ҫʹ��ABC���ADE���ƣ������������������еģ�������| A�� | $\frac{AC}{AD}$=$\frac{AB}{AE}$ | B�� | $\frac{AC}{AD}$=$\frac{BC}{DE}$ | C�� | $\frac{AC}{AD}$=$\frac{AB}{DE}$ | D�� | $\frac{AC}{AD}$=$\frac{BC}{AE}$ |
13����֪m=n�����е�ʽ���������ǣ�������
| A�� | 3m=3n | B�� | $\frac{m}{4}$=$\frac{n}{4}$ | C�� | -m+2=-n+2 | D�� | m+1=n-1 |
 ��ͼ����֪A��B��C��D�ĵ㣬��������Ҫ��ͼ��
��ͼ����֪A��B��C��D�ĵ㣬��������Ҫ��ͼ�� ��ͼ����?ABCD�У�AE��BC������ΪE�����AB=5��BC=8��sinB=$\frac{4}{5}$����ôtan��CDE=$\frac{1}{2}$��
��ͼ����?ABCD�У�AE��BC������ΪE�����AB=5��BC=8��sinB=$\frac{4}{5}$����ôtan��CDE=$\frac{1}{2}$�� ��ͼ�������ʵ�������ϵ��д��ͼ�м����ؼ�������꣮
��ͼ�������ʵ�������ϵ��д��ͼ�м����ؼ�������꣮