题目内容
7.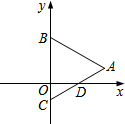 如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )| A. | (1,2$\sqrt{3}$) | B. | (2,2$\sqrt{3}$) | C. | (2$\sqrt{3}$,1) | D. | (2$\sqrt{3}$,2) |
分析 先过点A作AE⊥OB,根据△ABC是等边三角形,求出AE,再根据点D的坐标,得出点A的坐标.
解答 解:过点A作AE⊥OB,如图:
∵点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),
∴AE=2$\sqrt{3}$,
$\frac{OD}{AE}=\frac{OC}{EC}$,
可得:$\frac{\sqrt{3}}{2\sqrt{3}}=\frac{OC}{2}$,
解得:OC=1,
OE=EC-OC=2-1=1,
所以点A的坐标为(2$\sqrt{3}$,1),
故选C.
点评 此题考查了等边三角形的性质,用到的知识点是勾股定理,关键是作出辅助线,求出点A的坐标.

练习册系列答案
相关题目
2. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )| A. | (45,13) | B. | (45,9) | C. | (45,22) | D. | (45,0) |
12.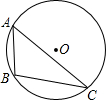 如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
 如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )| A. | 2π | B. | 4π | C. | 6π | D. | 12π |
16.据统计2015年宁波市实现地区生产总值8011.5亿元,按可比价格计算,比上年增长了8%,把8011.5亿用科学记数法表示是( )
| A. | 8011.5×108 | B. | 801.15×109 | C. | 8.0115×1010 | D. | 8.0115×1011 |
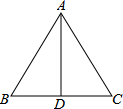 等边三角形ABC中,边长AB=6,则高AD的长度为3$\sqrt{3}$.
等边三角形ABC中,边长AB=6,则高AD的长度为3$\sqrt{3}$. 推理填空:如图,根据图形填空
推理填空:如图,根据图形填空 如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).
如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017). 如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π.
如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π. 在“世界粮食日”前夕,某校团委随机抽取了n名本校学生,对某日午餐剩饭菜情况进行问卷调查.问卷中的剩饭菜情况包括:
在“世界粮食日”前夕,某校团委随机抽取了n名本校学生,对某日午餐剩饭菜情况进行问卷调查.问卷中的剩饭菜情况包括: