题目内容
17．
在“世界粮食日”前夕，某校团委随机抽取了n名本校学生，对某日午餐剩饭菜情况进行问卷调查．问卷中的剩饭菜情况包括：A．饭和菜全部吃完； B．饭有剩余但菜吃完；
C．饭吃完但菜有剩余；D．饭和菜都有剩余．
每位学生在问卷调查时都按要求只选择了其中一种情况，该校团委收回全部问卷后，将收集到的数据整理并绘制成如下的条形统计图．
（1）求n的值．
（2）饭和菜全部吃完的学生人数占被调查的学生人数的百分比为60%．
（3）根据统计结果，估计该校2400名学生中菜有剩余的学生人数．
分析 （1）根据条形图，把A，B，C，D的人数加起来，即可解答；
（2）用A的人数÷总人数，即可得到百分比；
（3）用样本中菜有剩余即C、D人数所占比例×2400可得．
解答 解：（1）n=120+40+20+20=200；
（2）$\frac{120}{200}$×100%=60%；
（3）2400×$\frac{20+20}{200}$=480（人），
答：估计该校2400名学生中菜有剩余的学生约为480人．
故答案为：（2）60%．
点评 本题考查的是条形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
练习册系列答案
相关题目
7．
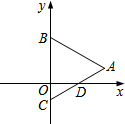如图，在平面直角坐标系中，点B、C在y轴上，△ABC是等边三角形，AB=4，AC与x轴的交点D的坐标是（$\sqrt{3}$，0），则点A的坐标为（ ）
如图，在平面直角坐标系中，点B、C在y轴上，△ABC是等边三角形，AB=4，AC与x轴的交点D的坐标是（$\sqrt{3}$，0），则点A的坐标为（ ）| A． | （1，2$\sqrt{3}$） | B． | （2，2$\sqrt{3}$） | C． | （2$\sqrt{3}$，1） | D． | （2$\sqrt{3}$，2） |
8．马老师想知道学生每天上学路上要花多少时间，于是让大家将每天来校的单程时间写在纸上用于统计，下面是全班45名学生单程所花时间（单位：分）与对应人数（单位：人）的统计表，则关于这45名学生单程所花时间的数据的中位数是（ ）
| 单程所花时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 人数 | 6 | 6 | 8 | 14 | 5 | 4 | 1 | 1 |
| A． | 15 | B． | 20 | C． | 25 | D． | 30 |
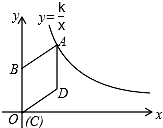如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y=$\frac{k}{x}$（x＞0）的图象上，点D的坐标为（4，3）．
12．使得二次根式$\sqrt{3-4x}$有意义的字母x的取值范围是（ ）
| A． | x≥$\frac{3}{4}$ | B． | x≤$\frac{3}{4}$ | C． | x＜$\frac{3}{4}$ | D． | x≠$\frac{3}{4}$ |
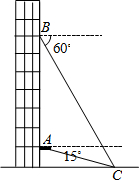从一幢建筑大楼的两个观察点A，B观察地面的花坛（点C），测得俯角分别为15°和60°，如图，直线AB与地面垂直，AB=50米，试求出点B到点C的距离．（结果保留根号）