题目内容
2. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )| A. | (45,13) | B. | (45,9) | C. | (45,22) | D. | (45,0) |
分析 将其左侧相连,看作正方形边上的点.分析边上点的个数得出规律“边长为n的正方形有2n+1个点”,将边长为n的正方形边上点与内部点相加得出共有(n+1)2个点,由此规律结合图形的特点可以找出第2016个点的坐标.
解答 解:将其左侧相连,看作正方形边上的点,如图所示.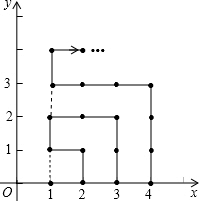
边长为0的正方形,有1个点;边长为1的正方形,有3个点;边长为2的正方形,有5个点;…,
∴边长为n的正方形有2n+1个点,
∴边长为n的正方形边上与内部共有1+3+5+…+2n+1=(n+1)2个点.
∵2016=45×45-9,
结合图形即可得知第2016个点的坐标为(45,9).
故选B.
点评 本题考查了规律型中的点的坐标,解题的规律是找出“边长为n的正方形边上点与内部点相加得出共有(n+1)2个点”.本题属于中档题,有点难度,解决该题型题目时,补充完整图形,将其当成正方形边上的点来看待,本题的难点在于寻找第2016个点所在的正方形的边是平行与x轴的还是平行y轴的.

练习册系列答案
相关题目
7.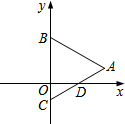 如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )
 如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )| A. | (1,2$\sqrt{3}$) | B. | (2,2$\sqrt{3}$) | C. | (2$\sqrt{3}$,1) | D. | (2$\sqrt{3}$,2) |
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.使得二次根式$\sqrt{3-4x}$有意义的字母x的取值范围是( )
| A. | x≥$\frac{3}{4}$ | B. | x≤$\frac{3}{4}$ | C. | x<$\frac{3}{4}$ | D. | x≠$\frac{3}{4}$ |
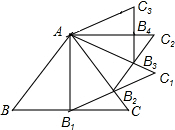 如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..
如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..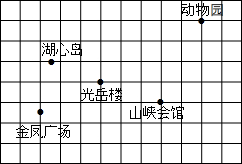 如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.
如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.