题目内容
6.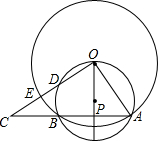 如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.
如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.(1)求⊙P的半径长;
(2)当△AOC为直角三角形时,求线段OD的长;
(3)设线段OD的长度为x,线段CE的长度为y,求y与x之间的函数关系式及其定义域.
分析 (1)首先设OP的延长线交AB于点H,连接AP,由垂径定理可求得AH的长,然后由三角函数,求得OH的长,再设⊙P的半径为r,由在Rt△AHP中,AH2+PH2=AP2,即可求得答案;
(2)首先过点P作PG⊥OD于点G,求得OA的长,易证得△PGO∽△OHA,然后由相似三角形的对应边成比例,求得答案;
(3)首先过点H作HI⊥OC于点I,可得PG∥HI,然后由平行线分线段成比例定理,求得OI,再由△OHI∽△OCH,求得答案.
解答 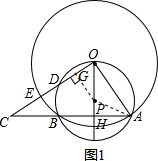 解:(1)设OP的延长线交AB于点H,连接AP,
解:(1)设OP的延长线交AB于点H,连接AP,
∵AH=$\frac{1}{2}$AB=$\frac{1}{2}$×24=12,tan∠AOP=$\frac{2}{3}$,
∴OH=$\frac{AH}{tan∠AOP}$=18,
设⊙P的半径为r,
在Rt△AHP中,AH2+PH2=AP2,
∴(18-r)2+122=r2,
解得:r=13,
答:⊙P的半径长为13;
(2)过点P作PG⊥OD于点G,
则OA=$\sqrt{A{H}^{2}+O{H}^{2}}$=$\sqrt{1{2}^{2}+1{8}^{2}}$=6$\sqrt{13}$,
∵∠AOC=90°,
∴∠POG+∠AOH=90°,
∵∠AOH+∠OAH=90°,
∴∠POG=∠OAH,
∴△PGO∽△OHA,
∴$\frac{OG}{AH}=\frac{OP}{OA}$,
即$\frac{OG}{12}$=$\frac{13}{6\sqrt{13}}$,
解得:OD=4$\sqrt{13}$;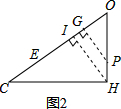 (3)如图2,过点H作HI⊥OC于点I,则OE=OA=6$\sqrt{13}$,
(3)如图2,过点H作HI⊥OC于点I,则OE=OA=6$\sqrt{13}$,
∴PG∥HI,
∴$\frac{OG}{OI}=\frac{OP}{OH}$,
即$\frac{\frac{1}{2}x}{OI}=\frac{13}{18}$,
∴OI=$\frac{9}{13}$x,
∵∠O是公共角,∠OUH=∠OHC=90°,
∴△OHI∽△OCH,
∴$\frac{OH}{OC}=\frac{OI}{OH}$,
∴$\frac{18}{\frac{9}{13}x}=\frac{y+6\sqrt{13}}{18}$,
∴y=$\frac{468}{x}$-6$\sqrt{13}$(0<x<6$\sqrt{13}$).
点评 此题属于圆的综合题.考查了切线的判定与性质、相似三角形的判定与性质、平行线分线段成比例定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案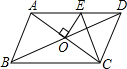 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
| A. | a=b | B. | a=0 | C. | ab=1 | D. | a+b=0 |
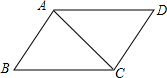 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
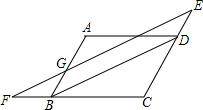 如图,在?ABCD中,直线EF∥BD,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H.
如图,在?ABCD中,直线EF∥BD,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H. 如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )
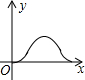
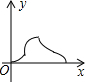
如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )
 已知:抛物线y=x2+bx+c经过点A(2,-3)和B(4,5).
已知:抛物线y=x2+bx+c经过点A(2,-3)和B(4,5).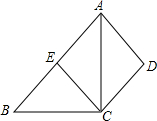 如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.