题目内容
4.二次函数y=ax2上的点B、C与x轴上的点A(-5,0),D(3,0)构成平行四边形ABCD,BC与y轴交于点E(0,6),则实数a=$\frac{3}{8}$.分析 由于四边形ABCD是平行四边形,则BC=AD=8,根据抛物线的对称性知:C、B关于y轴对称,由此可得到C、B的坐标,代入抛物线的解析式中即可求出待定系数a的值.
解答 解:由题意知:OA=5,OD=3,
∴AD=OA+OD=8,
∴BC=AD=10;
∵E(0,6),
∵由对称性知:B(-4,6),C(4,6);
将C(4,6)代入y=ax2,得a=$\frac{6}{16}$=$\frac{3}{8}$;
故答案为:$\frac{3}{8}$.
点评 此题主要考查了抛物线的对称性、平行四边形的判定以及用待定系数法求二次函数解析式的方法;由抛物线的对称性得出点B、C的坐标是解决问题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
5.将直线y=$\frac{1}{2}$x+1向右平移4个单位长度后得到直线y=kx+b,则k,b对应的值是( )
| A. | $\frac{1}{2}$,1 | B. | -$\frac{1}{2}$,1 | C. | -$\frac{1}{2}$,-1 | D. | $\frac{1}{2}$,-1 |
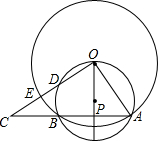 如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.
如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.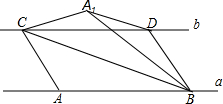 如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.
如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.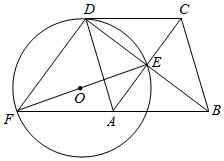 如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.
如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.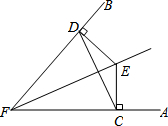 已知:E是∠AFB的平分线上一点,EC⊥FA,ED⊥FB,垂足分别为C、D.求证:FE是CD的垂直平分线.
已知:E是∠AFB的平分线上一点,EC⊥FA,ED⊥FB,垂足分别为C、D.求证:FE是CD的垂直平分线.