题目内容
11.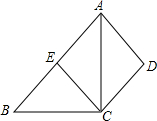 如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.(1)求证:四边形AECD是菱形;
(2)如果点E是AB的中点,AC=4,EC=2.5,求四边形ABCD的面积.
分析 (1)由“邻边相等的平行四边形为菱形”进行证明;
(2)根据菱形的性质和等腰三角形的性质推知△ABC是直角三角形,所以结合直角三角形的面积求法和图形得到:四边形ABCD的面积=S△AEC+S△EBC+S△ACD.
解答 (1)证明:∵AB∥CD,CE∥AD,
∴四边形AECD是平行四边形,…(1分);
∵AC平分∠BAD,
∴∠EAC=∠DAC,
∵AB∥CD,
∴∠EAC=∠ACD,
∴∠DAC=∠ACD,
∴AD=CD,
∴四边形AECD是菱形.
(2)解:∵四边形AECD是菱形,
∴AE=CE,
∴∠EAC=∠ACE,
∵点E是AB的中点,
∴AE=BE,
∴∠B=∠ECB,
∴∠ACE+∠ECB=90°,即∠ACB=90°;
∵点E是AB的中点,EC=2.5,
∴AB=2EC=5,
∴BC=3.
∴S△ABC=$\frac{1}{2}$BC•AC=6.
∵点E是AB的中点,四边形AECD是菱形,
∴S△AEC=S△EBC=S△ACD=3.
∴四边形ABCD的面积=S△AEC+S△EBC+S△ACD=9.
点评 本题考查了菱形的判定与性质.解答(2)题时,利用了菱形的性质、直角三角形的判定等知识点,借用了“分割法”求得四边形ABCD的面积.

练习册系列答案
相关题目
19.在平行四边形ABCD中,∠A:∠B:∠C=2:1:2,则∠D=( )
| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
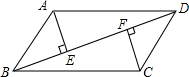 如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.
如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.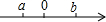 实数a、b在数轴上对应点的位置如图所示:则3a-$\sqrt{(a-b)^{2}}$=4a-b.
实数a、b在数轴上对应点的位置如图所示:则3a-$\sqrt{(a-b)^{2}}$=4a-b.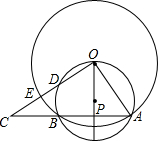 如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.
如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.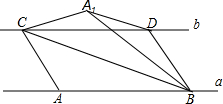 如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.
如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC. 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上)
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上)