题目内容
10.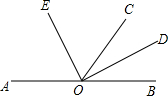 如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.(1)分别指出图中∠AOD的补角,∠BOE的补角
(2)若∠BOC=68°,求∠COD和∠EOC的度数
(3)直接写出∠BOD与∠AOE的数量关系.
分析 (1)根据互为补角的和等于180°找出即可;
(2)先求出∠AOC的度数,再根据角平分线的定义解答;
(3)根据角平分线的定义表示出∠BOD与∠AOE,然后整理即可得解.
解答 解:(1)∠AOD的补角是∠BOD∠COD,∠BOE的补角是∠AOE和∠COE;
(2)∵∠BOC=68°,
∴∠AOC=180°-∠BOC=180°-68°=112°,
∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=34°,∠COE=56°;
(3)∵OD平分∠BOC,OE平分∠AOC,
∴∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOD+∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOD与∠AOE互余.
点评 本题考查了余角和补角的概念,角度的计算,以及角平分线的定义,准确识图并熟记概念是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若x+3是4的平方根,则x的值为( )
| A. | -1 | B. | ±1 | C. | -2 | D. | -1或-5 |
20.已知A、B、C三点在同一直线上,AB=16,BC=10,M、N分别是AB、BC的中点,则MN等于( )
| A. | 2 | B. | 13 | C. | 3或13 | D. | 3 |
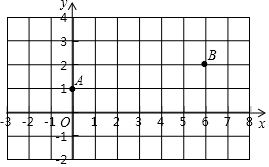 如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2. 如图,⊙O的内接△ABC中,已知BC=3,∠A=60°,求⊙O的半径长.
如图,⊙O的内接△ABC中,已知BC=3,∠A=60°,求⊙O的半径长. 如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,求△BEQ周长的最小值?
如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,求△BEQ周长的最小值?