题目内容
15.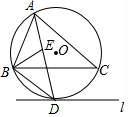 如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC.
如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC.(1)求证:AD平分∠BAC;
(2)作∠ABC的平分线BE交AD于点E,求证:BD=DE.
分析 (1)连接OD,由直线l与⊙O相切于点D可得出OD⊥l,结合l∥BC即可得出OD⊥BC,再根据垂径定理即可得出$\widehat{BD}$=$\widehat{CD}$,进而可得出∠BAD=∠CAD,即AD平分∠BAC;
(2)由角平分线的定义结合(1)的结论即可得出∠CBD+∠CBE=∠BAE+∠ABE,再根据三角形外角的性质即可得出∠EBD=∠DEB,由此即可证出BD=DE.
解答 证明:(1)连接OD,如图所示.
∵直线l与⊙O相切于点D,
∴OD⊥l.
∵l∥BC,
∴OD⊥BC,
∴$\widehat{BD}$=$\widehat{CD}$,
∴∠BAD=∠CAD,
∴AD平分∠BAC;
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE.
又∵$\widehat{BD}$=$\widehat{CD}$,
∴∠BAD=∠CBD,
∴∠CBD+∠CBE=∠BAE+∠ABE.
又∵∠DEB=BAE+∠ABE,
∴∠EBD=∠DEB,
∴BD=DE.
点评 本题考查了切线的性质、垂径定理、圆周角定理以及角平分线的定义,通过角的计算找出∠BAD=∠CAD(∠EBD=∠DEB)是解题的关键.

练习册系列答案
相关题目
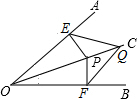 已知OC平分∠AOB,点P,Q都是OC上不同的点,PE⊥OA,PF⊥OB,连接EQ,FQ,求证:FQ=EQ.
已知OC平分∠AOB,点P,Q都是OC上不同的点,PE⊥OA,PF⊥OB,连接EQ,FQ,求证:FQ=EQ.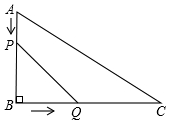 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问:
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问: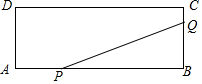 如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).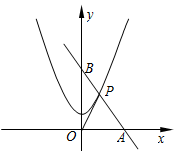 已知,如图,直线AB经过点B(0,6),且tan∠ABO=$\frac{2}{3}$,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.
已知,如图,直线AB经过点B(0,6),且tan∠ABO=$\frac{2}{3}$,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.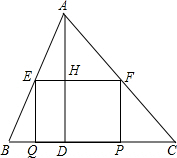 如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.