题目内容
11.已知k=$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$,则k=1或-2;若n2+16+$\sqrt{m+6}$=8n,则关于x的一次函数y=kx+n-m的图象一定经过第一、二象限.分析 根据k=$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$即可得出k=1或-2,由n2+16+$\sqrt{m+6}$=8n利用偶次方及被开方数非零即可得出m、n的值,进而可得出n-m的值,再根据一次函数图象与系数的关系即可得出一次函数经过的象限,此题得解.
解答 解:∵k=$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$,
∴a=b=c,k=1或a+b=-c,k=-2.
∵n2+16+$\sqrt{m+6}$=8n,
∴(n-4)2+$\sqrt{m+6}$=0,
∴m=-6,n=4,
∴n-m=10>0,
∴一次函数y=kx+n-m的图象经过第一、二、三象限或第一、二、四象限.
故答案为:1或-2;一、二.
点评 本题考查了一次函数图象与系数的关系以及偶次方及被开方数非零,通过解方程组以及偶次方和被开方数非零求出k和n-m的值是解题的关键.

练习册系列答案
相关题目
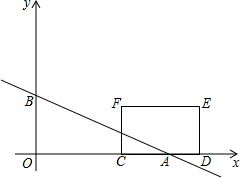 如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.
如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.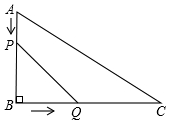 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问:
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问: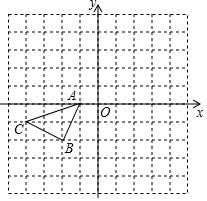 在直角坐标系中,△ABC的三个顶点的位置如图所示:
在直角坐标系中,△ABC的三个顶点的位置如图所示: