题目内容
14.计算:(1)|-4|-(-3)2$÷\frac{1}{3}$-20100
(2)$\sqrt{2}$(2cos45°-sin60°)+$\frac{\sqrt{24}}{4}$.
分析 (1)利用绝对值以及零指数幂的性质化简进而求出即可;
(2)利用特殊角的三角函数值进而代入化简求出即可.
解答 解:(1)|-4|-(-3)2$÷\frac{1}{3}$-20100
=4-9×3-1
=-24;
(2)$\sqrt{2}$(2cos45°-sin60°)+$\frac{\sqrt{24}}{4}$
=$\sqrt{2}$(2×$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{2}$)+$\frac{\sqrt{6}}{2}$
=2-$\frac{\sqrt{6}}{2}$+$\frac{\sqrt{6}}{2}$
=2.
点评 此题主要考查了二次根式的混合运算以及特殊角的三角函数值等知识,正确化简二次根式是解题关键.

练习册系列答案
相关题目
6.函数y=$\frac{1-k}{x}$的图象与直线y=-x没有交点,那么k的取值范围是( )
| A. | k>1 | B. | k<1 | C. | k>-1 | D. | k<-1 |
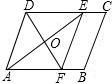 如图,在?ABCD中,AE是∠DAB的平分线,EF∥AD交B于点F,连接DF交AE于点O,
如图,在?ABCD中,AE是∠DAB的平分线,EF∥AD交B于点F,连接DF交AE于点O,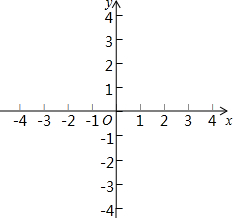 平面直角坐标系中,标出并顺次连结A(-2,1),B(-2,-1),C(2,1),D(2,3)各点,你会得到一个什么图形?试求出该图形的面积.
平面直角坐标系中,标出并顺次连结A(-2,1),B(-2,-1),C(2,1),D(2,3)各点,你会得到一个什么图形?试求出该图形的面积.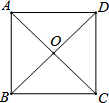 如图,正方形ABCD的对角线交于点O,点F是BC的中点.
如图,正方形ABCD的对角线交于点O,点F是BC的中点. 如图,△ABC中,∠BAC=120°,AB=AC,BC=6,请你建立适当的平面直角坐标系,并写出A,B,C各点的坐标.
如图,△ABC中,∠BAC=120°,AB=AC,BC=6,请你建立适当的平面直角坐标系,并写出A,B,C各点的坐标.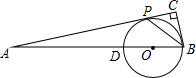 如图,在△ABC中,∠ACB=90°,点P是AC上一点,且BP平分∠ABC,点D是AB上一点,以BD为直径的⊙O经过点P.
如图,在△ABC中,∠ACB=90°,点P是AC上一点,且BP平分∠ABC,点D是AB上一点,以BD为直径的⊙O经过点P.